भुजा a वाले एक समबाहु त्रिभुज के शीर्ष A और B पर समान आवेश q है। त्रिभुज के बिंदु C पर विद्युत् क्षेत्र का परिमाण ज्ञात कोजिए।
माना बिंदु C पर एक परीक्षण आवेश +Q है।
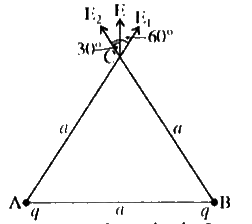
चूँकि यह एक समबाहु त्रिभुज है और बिंदु A तथा B पर समान आवेश है अतः
E1=E2=Kqa2
अतः परिणामी विद्युत् क्षेत्र की तीरवता का मान
E=√E21+E22+2E1E2cos60∘
=√(Kqa2)2+(Kqa2)2+2(Kqa2)(Kqa2)12
=√3(Kqa2)2
=√3Kqa2
Topper's Solved these Questions
- BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - अन्य महत्तवपूर्ण प्रश्न54videos
विधुत क्षेत्र
- BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - निबन्धात्मक प्रश्न-5videos
विधुत क्षेत्र
- BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत विभव EXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न - )10videos
विद्युत विभव
- BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत धारिता EXERCISE - आंकिक प्रश्न (उच्चस्तरीय बुद्धि-कौशल्य प्रश्न )2videos
विधुत धारिता
Similar Questions
किसी विद्युत द्विध्रुव के निरक्षीय रेखा पर स्थित बिंदु पर विद्युत क्षेत्र की दिशा क्या होती है?
07:55View Solutionदो आवेशों के मध्य स्थिर विद्युत बल के कूलॉम के नियम को परिभाषित कीजिये तथा इसकी सीमायें बताइ़ए। इस नियम द्वारा इकाई आवेश की परिभाषा दीजिए।
07:05View Solutionबाह्य क्षेत्र में विद्युत द्विध्रुव की स्थितिज ऊर्जा की विभन्न स्थितियों का वर्णन कीजिए और चित्र भी बनाइए |
02:37View Solutionn समरूप संधारित्र समांतर क्रम में जुड़े हुए है | उन्हें V विभव तक आवेशित किया जाता है अब इन्हे अलग - अलग करके श्रेणीक्रम में जोड़ दिया जाता है | सिद्ध कीजिए की दोनों दशाओं में संयोजन की ऊर्जा समान रहती है |
48:35View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
02:54View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
02:17View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
03:33View Solutionविद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
06:51View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
05:09View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
03:17View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
03:50View SolutionA(a,0) और B(−a,0)दो स्थिर बिंदु है । त्रिभुज ABC के शीर्ष C का बिन्दुपथ ज्ञात कीजिए यदि ∠A−∠B=θ.
02:40View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
02:39View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
04:32View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
03:50View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
45:31View Solution

