S and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
Step by step video & image solution for S and T are points on the sides PQ and PR, respectively of Delta PQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of Delta PST and Delta PQR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.
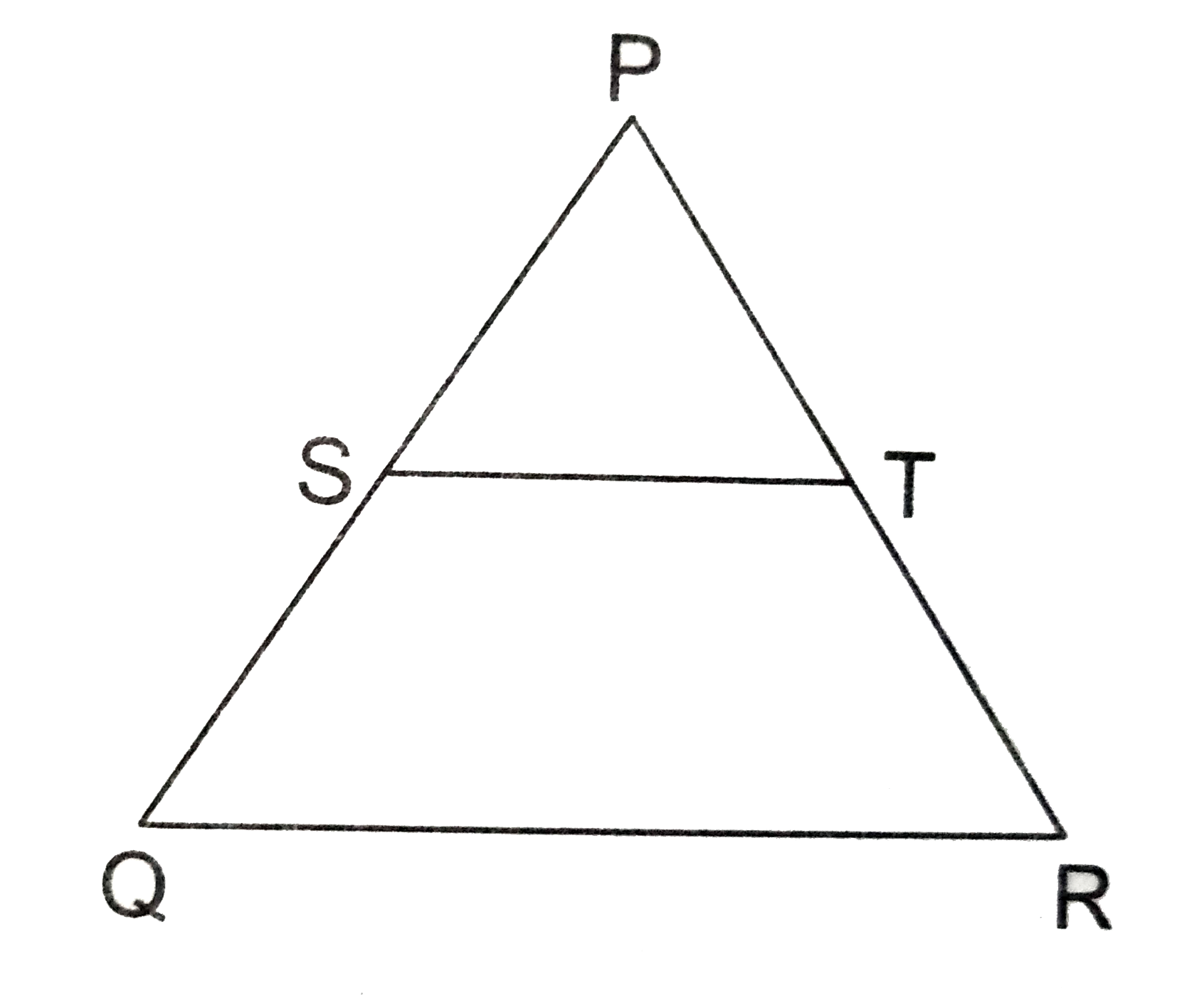
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View Solution
Knowledge Check
In the triangle PQR below, - S and T are 2 points on the sides RP and RQ respectively such that ST is parallel to PQ.
- The ratio of RT to TQ is 1:2.
The area of ΔRST = 100 sq. units.
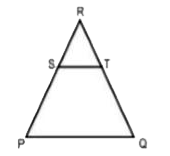
What is the area of PQTS?A200 sq. unitsB300 sq. unitsC600 sq. unitsD800 sq. unitsIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
A5 cmB6 cmC313cmD413cmIn △PQR L and M are two points on the sides PQ and PR respectively such that LMII QR. If PL = 2cm, LQ = 6 cm and PM= 1.5 cm, then MR (in cm) is
A0.5B4.5C9D8
S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionS and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
View SolutionIn △PQR ,PQ=24 cm and ∠Q=58∘. S and T are points on side PQ and PR, respectively such that ∠STR=122∘. If PS=14cm and PT= 12cm, then the length of RT is:
त्रिभुज PQR में, PQ = 24 सेमी तथा ∠Q=58∘ है|S और T क्रमशः भुजा PQ तथा PR पर स्थित ऐसे बिंदु हैं कि ∠STR=122∘ है |यदि PS = 14 सेमी तथा PT =12 सेमी है, तो RT की लंबाई कितनी होगी ?
View Solution