In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of , then find the lengths of sides PQ and PR.
To solve the problem step by step, we need to find the lengths of sides PQ and PR of triangle PQR, given the radius of the inscribed circle and the lengths of segments QT and TR.
Step 1: Understand the given information
- The radius of the incircle (r) = 6 cm
- Length of QT = 12 cm
- Length of TR = 9 cm
- Area of triangle PQR = 189 cm²
Step 2: Find the length of QR
Since QT and TR are segments of QR, we can find the length of QR:
QR=QT+TR=12cm+9cm=21cm
Step 3: Use the area formula involving the radius of the incircle
The area (A) of triangle PQR can also be expressed in terms of the semi-perimeter (s) and the radius of the incircle (r):
A=r×s
Where s is the semi-perimeter:
s=PQ+PR+QR2
Step 4: Set up the equations
Let PQ=a and PR=b. Then, we can express the semi-perimeter:
s=a+b+212
Substituting into the area formula:
189=6×(a+b+212)
Simplifying this gives:
189=3(a+b+21)
189=3a+3b+63
3a+3b=189−63
3a+3b=126
a+b=42(Equation 1)
Step 5: Express PQ and PR in terms of the tangents
From the properties of tangents drawn from a point outside the circle, we have:
- Let PA=x (where A is the point of contact on side PQ)
- Then QA=QT=12 cm, so PQ=PA+QT=x+12
- Let PB=y (where B is the point of contact on side PR)
- Then RB=TR=9 cm, so PR=PB+TR=y+9
Step 6: Substitute into Equation 1
Substituting these expressions into Equation 1:
(x+12)+(y+9)=42
x+y+21=42
x+y=21(Equation 2)
Step 7: Solve the system of equations
Now we have two equations:
1. a+b=42
2. x+y=21
From Equation 1, we know:
PQ=x+12andPR=y+9
Substituting y=21−x into the expression for PR:
PR=(21−x)+9=30−x
Step 8: Find PQ and PR
Now substituting back into the lengths:
1. PQ=x+12
2. PR=30−x
Step 9: Find the values of PQ and PR
To find the specific lengths, we can express PQ and PR in terms of x:
- If x=12, then:
PQ=12+12=24cm
PR=30−12=18cm
Final Answer
Thus, the lengths of sides PQ and PR are:
- PQ=24cm
- PR=18cm
- The radius of the incircle (r) = 6 cm
- Length of QT = 12 cm
- Length of TR = 9 cm
- Area of triangle PQR = 189 cm²
Since QT and TR are segments of QR, we can find the length of QR:
QR=QT+TR=12cm+9cm=21cm
The area (A) of triangle PQR can also be expressed in terms of the semi-perimeter (s) and the radius of the incircle (r):
A=r×s
Where s is the semi-perimeter:
s=PQ+PR+QR2
Let PQ=a and PR=b. Then, we can express the semi-perimeter:
s=a+b+212
Substituting into the area formula:
189=6×(a+b+212)
Simplifying this gives:
189=3(a+b+21)
189=3a+3b+63
3a+3b=189−63
3a+3b=126
a+b=42(Equation 1)
From the properties of tangents drawn from a point outside the circle, we have:
- Let PA=x (where A is the point of contact on side PQ)
- Then QA=QT=12 cm, so PQ=PA+QT=x+12
- Let PB=y (where B is the point of contact on side PR)
- Then RB=TR=9 cm, so PR=PB+TR=y+9
Substituting these expressions into Equation 1:
(x+12)+(y+9)=42
x+y+21=42
x+y=21(Equation 2)
Now we have two equations:
1. a+b=42
2. x+y=21
PQ=x+12andPR=y+9
Substituting y=21−x into the expression for PR:
PR=(21−x)+9=30−x
Now substituting back into the lengths:
1. PQ=x+12
2. PR=30−x
To find the specific lengths, we can express PQ and PR in terms of x:
- If x=12, then:
PQ=12+12=24cm
PR=30−12=18cm
Thus, the lengths of sides PQ and PR are:
- PQ=24cm
- PR=18cm
Topper's Solved these Questions
Similar Questions
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR=189cm2, then find the lengths of sides PQ and PR.
View SolutionIn the given figure, a triangle PQR is drawn to circumscribe a circle of radius √3cm such that segments RS and QS into which QR is divided by the point of contact S are of lengths 5cm and 3cm respectively. If the area of ΔPQR is 10√3cm2, then find the sides PQ and PR.
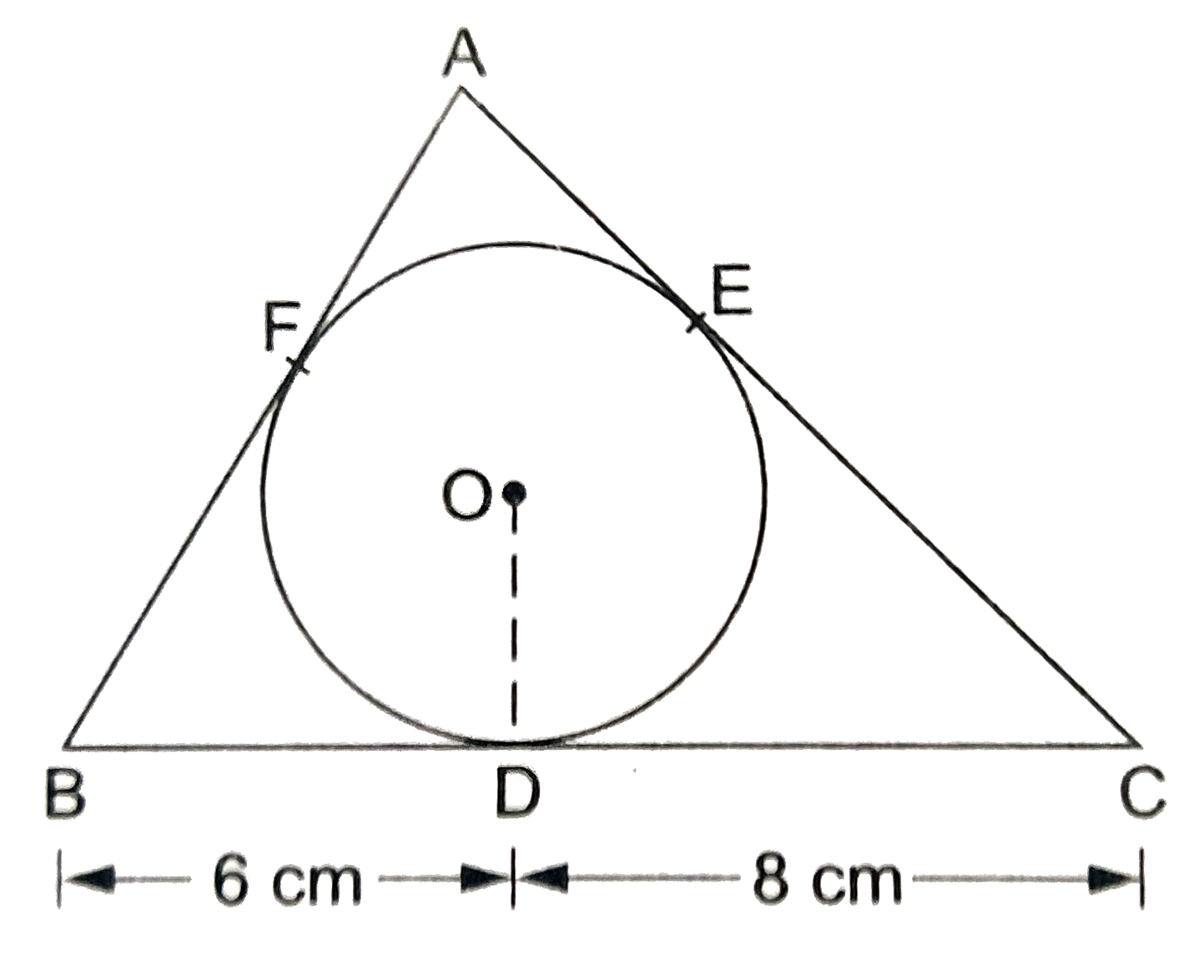
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6cm and 8cm respectively. Find the lengths of the sides AB and AC.
View SolutionQ25. Infig.,a triangle ABC is drawn to a circle of radius 3 cm, such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8cm respect Find the side AB if the area of ΔABC=63cm2
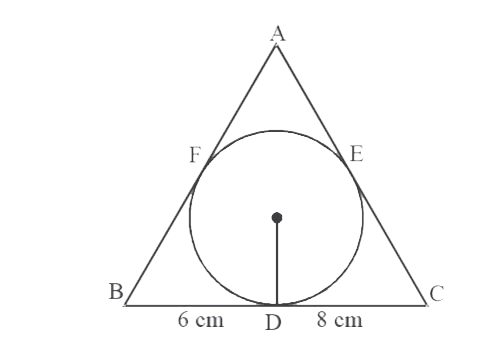
View SolutionIn the given figure ΔABC is drawn to circumscribe a circle of radius 3 cm, such that the segment BD and DC into which BC is divided by the point of contact D are of length 6 cm and 8 cm respectively, find side AB if the ar (ΔABC)=63cm2
View SolutionIn the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC are of lengths 6 cm and 9 cm respectively. If the area of △ABC=54cm2, then find the lengths of sides AB and AC. ltBRgt

View SolutionIn figure , a triangle ABC is drawn to circumscribe a circle of radius 3 cm , such that segments BD and DC are of length 6 cm and 9 cm .If the area of △ABC=54cm2, then find the lengths of the side AB and AC.

View SolutionThe perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then find the length of AB.
View SolutionIn Figure, A ABC is drawn to circumscribe a circle of radius 4cm such that the segments BDandDC are of lengths 8cm and 6cm respectively. Find the lengths of sides ABandAC, when area of ABC is 84cm2.
View SolutionIn ΔPQR ∠R=∠P and QR=4cm and PR=5cm Then the length of PQ is
View Solution
