A truck moving on horizontal road east with velocity collides elastically with a light ball moving with velocity along west. The velocity of the ball just after collision
65 m towards east
25 m towards wast
65 m towards wast
20 m towards east
The correct Answer is:A
To solve the problem of finding the velocity of the ball just after the elastic collision with the truck, we will use the principles of conservation of momentum and conservation of kinetic energy.
1. Identify the Given Information:
- Velocity of the truck (V_t) = 20 m/s (East)
- Velocity of the ball (V_b) = -25 m/s (West, taken as negative for direction)
- Mass of the truck (M) = M (we can assume it to be M)
- Mass of the ball (m) = m (we can assume it to be m)
2. Conservation of Momentum:
The total momentum before the collision is equal to the total momentum after the collision.
M⋅Vt+m⋅Vb=M⋅V′t+m⋅V′b
Substituting the values:
M⋅20+m⋅(−25)=M⋅V′t+m⋅V′b
3. Conservation of Kinetic Energy:
Since the collision is elastic, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
12MV2t+12mV2b=12M(V′t)2+12m(V′b)2
Substituting the values:
12M(20)2+12m(−25)2=12M(V′t)2+12m(V′b)2
4. Solving the Equations:
From the momentum equation:
20M−25m=MV′t+mV′b
From the kinetic energy equation:
200M+312.5m=M(V′t)2+m(V′b)2
5. Assuming the Masses:
For simplicity, let’s assume M = 1 and m = 1 (the masses can be canceled out in the equations). This gives us:
20−25=V′t+V′b
−5=V′t+V′b
6. Using the Elastic Collision Formula:
For elastic collisions, we can also use the formula for the final velocities:
V′b=(m1−m2)(m1+m2)V1+2m2(m1+m2)V2
Here, m1=M (truck) and m2=m (ball):
V′b=(1−1)(1+1)⋅20+2⋅1(1+1)⋅(−25)
V′b=0+22⋅(−25)=−25
7. Final Result:
The velocity of the ball just after the collision is:
V′b=−25 m/s (West)
- Velocity of the truck (V_t) = 20 m/s (East)
- Velocity of the ball (V_b) = -25 m/s (West, taken as negative for direction)
- Mass of the truck (M) = M (we can assume it to be M)
- Mass of the ball (m) = m (we can assume it to be m)
The total momentum before the collision is equal to the total momentum after the collision.
M⋅Vt+m⋅Vb=M⋅V′t+m⋅V′b
Substituting the values:
M⋅20+m⋅(−25)=M⋅V′t+m⋅V′b
Since the collision is elastic, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
12MV2t+12mV2b=12M(V′t)2+12m(V′b)2
Substituting the values:
12M(20)2+12m(−25)2=12M(V′t)2+12m(V′b)2
From the momentum equation:
20M−25m=MV′t+mV′b
From the kinetic energy equation:
200M+312.5m=M(V′t)2+m(V′b)2
For simplicity, let’s assume M = 1 and m = 1 (the masses can be canceled out in the equations). This gives us:
20−25=V′t+V′b
−5=V′t+V′b
For elastic collisions, we can also use the formula for the final velocities:
V′b=(m1−m2)(m1+m2)V1+2m2(m1+m2)V2
Here, m1=M (truck) and m2=m (ball):
V′b=(1−1)(1+1)⋅20+2⋅1(1+1)⋅(−25)
V′b=0+22⋅(−25)=−25
The velocity of the ball just after the collision is:
V′b=−25 m/s (West)
Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass m moving with a speed u1 collides elasticity with another identical ball moving with velocity u2.
(a) Find the velocities of the balls after collision if the impact is direct.
(b) Find the angle between velocities after collision if they collide obliquely and u2=0
View Solution
Knowledge Check
A truck moving on horizontal road towards east with velocity 20ms1 collides elastically with a light ball moving with velocity 25ms−1 along west. The velocity of the ball just after collision
A65ms−1 towards eastB25ms−1 towards westC65ms−1 towards westD20ms−1 towards eastA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
Aboth the balls come to restBthe velocities are exchanged between the two ballsCboth of them move at right angles to the original line of motionDone ball comes to rest and another ball travels back with velocity 2vA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
A−v,2vB−2v,vCv,−2vD2v,−v
A heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,

View SolutionA ball of mass m moving with velocity V, makes a head on elastic collision with a ball of the same moving with velocity 2V towards it. Taking direction of V as positive velocities of the two balls after collision are.
View SolutionA small ball is projected horizontally between two large blocks. The ball is given a velocity Vms−1 and each of the large blocks move uniformly with a velocity of 2Vms−1. The ball collides elastically with the blocks. If the velocity of the blocks do not change due to the collision, then find out the velocity of the ball after the 2nd collision.
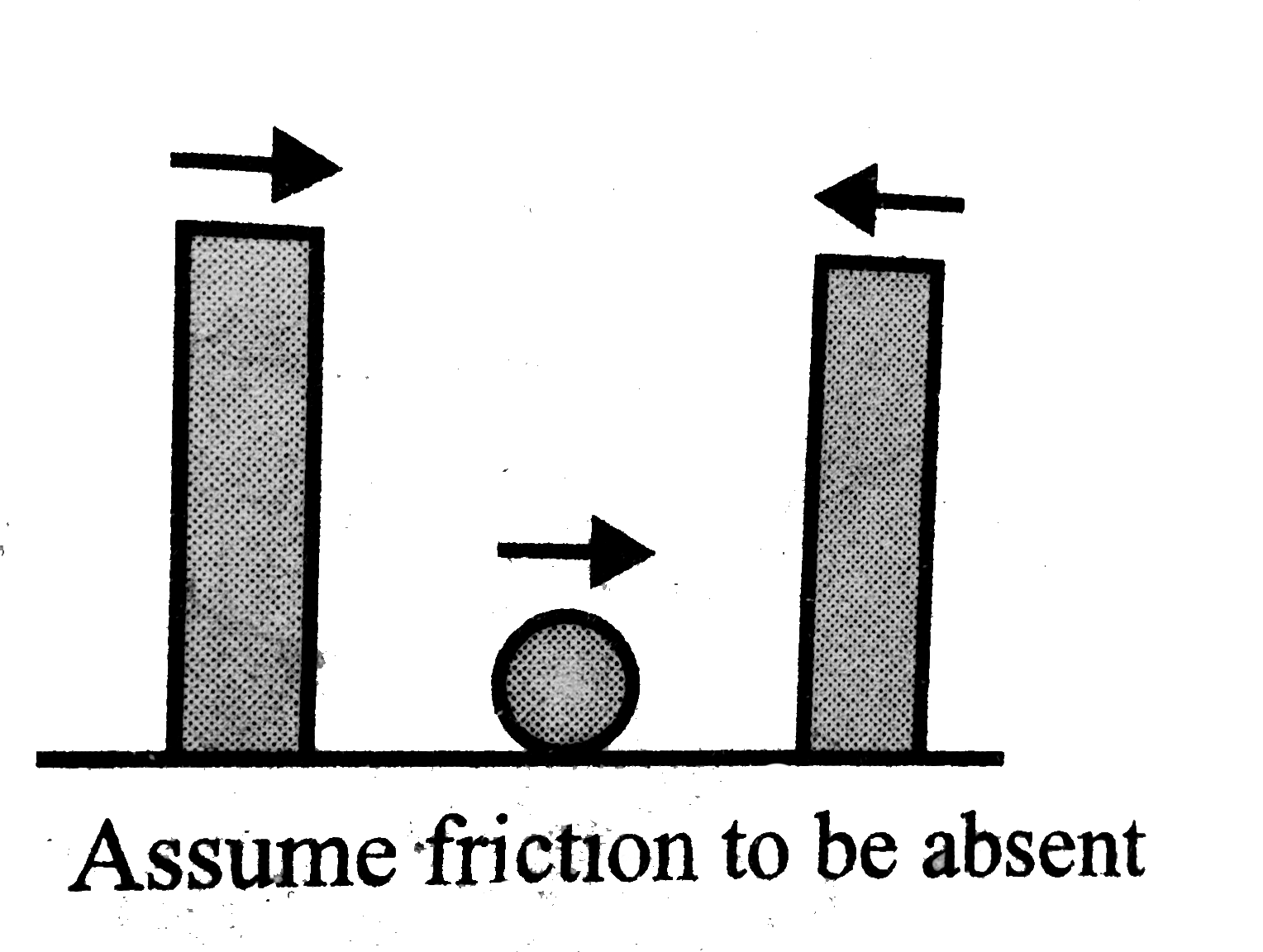
View SolutionA perfectly elastic ball P1 of mass 'm' moving with velocity v collides elastically with three exactly similar balls P2,P3,P4 lying smooth table. Velocity of the four balls after collision are
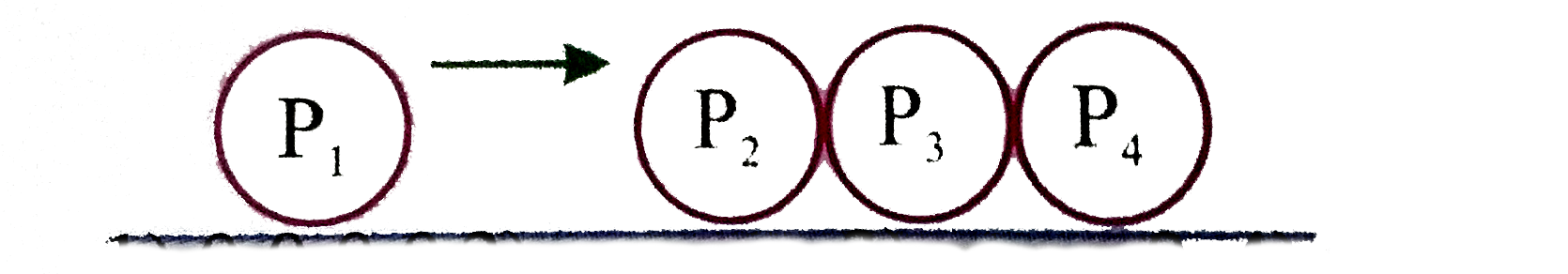 .
.
View Solution