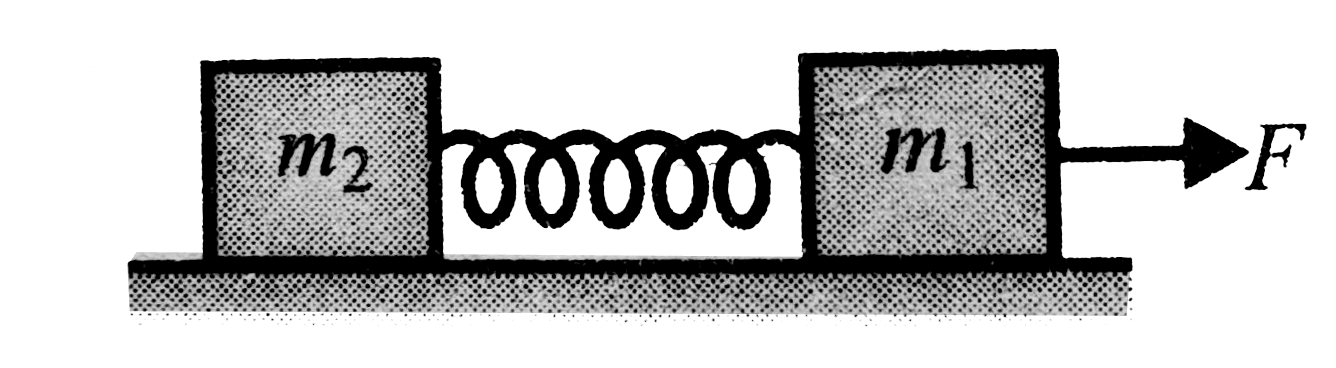
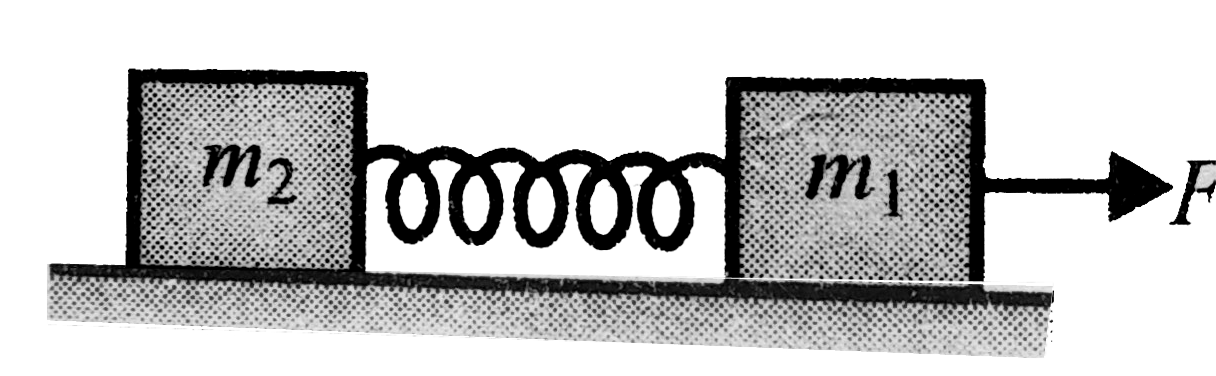
A system consists of two cubes of mass m1, and m2 respectively connected by a spring of force constant k. force (F) that should be applied to the upper cube for which the lower one just lifts after the force is removed, is
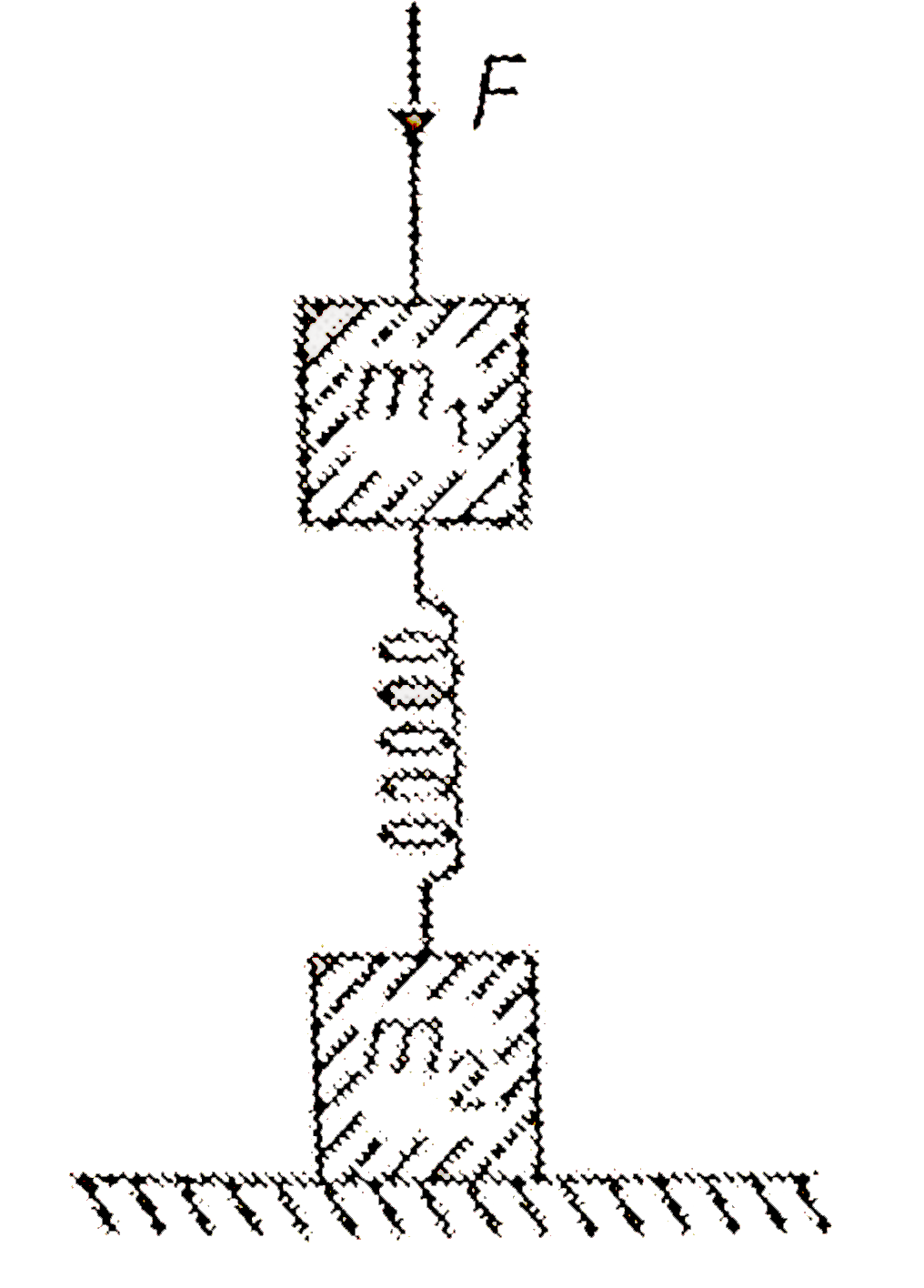
m1g
m1m2m1+m2g
(m1+m2)g
m2g
The correct Answer is:C
Step by step video & image solution for A system consists of two cubes of mass m_(1), and m_(2) respectively connected by a spring of force constant k. force (F) that should be applied to the upper cube for which the lower one just lifts after the force is removed, is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 3 Level-I
34 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 1
71 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
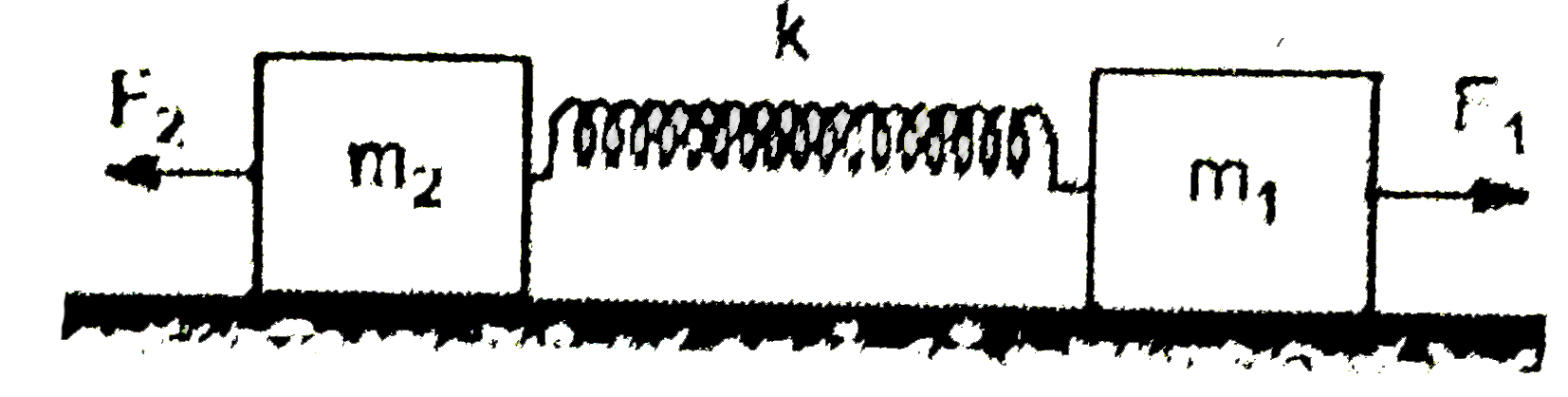
Two blocks of mass m1andm2 are connected by a spring of force constant k. Block of mass m1 os pulled by a constant force f2 [see fig 4E.19 (a)] find the maximum elongation in the spring .
View SolutionTwo disks of masses m1 and m2 are connected by a spring of force canstant k. The lower disk of mass m2lies on a table and the upper disk is vertically above it. What vertical force F should be applied to the upper disk so that when the force is withdraw, the lower disk is lifted off the table?
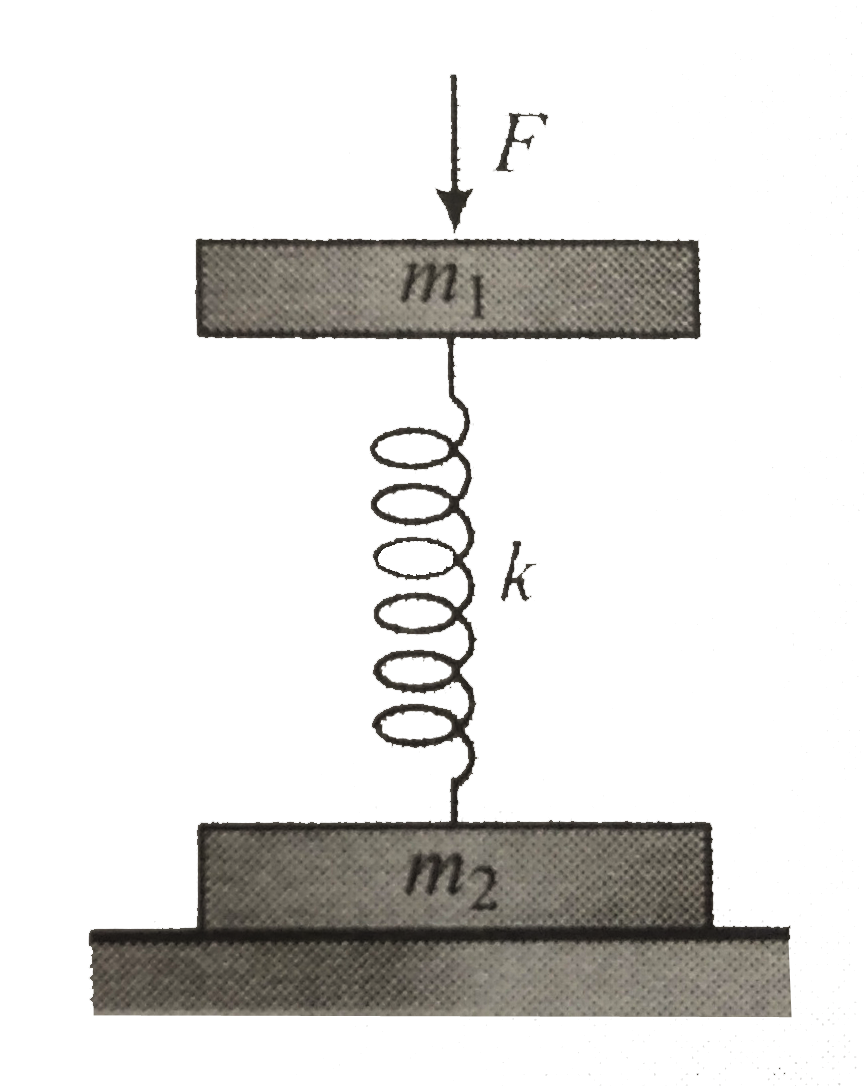
View Solution
Knowledge Check
The system of two weights with masses m1 and m2 are connected with weightless spring as shown. The system is resting on the support S. the support S is quickly removed. Find the accelerations of each of the weights right after the support S is removed.
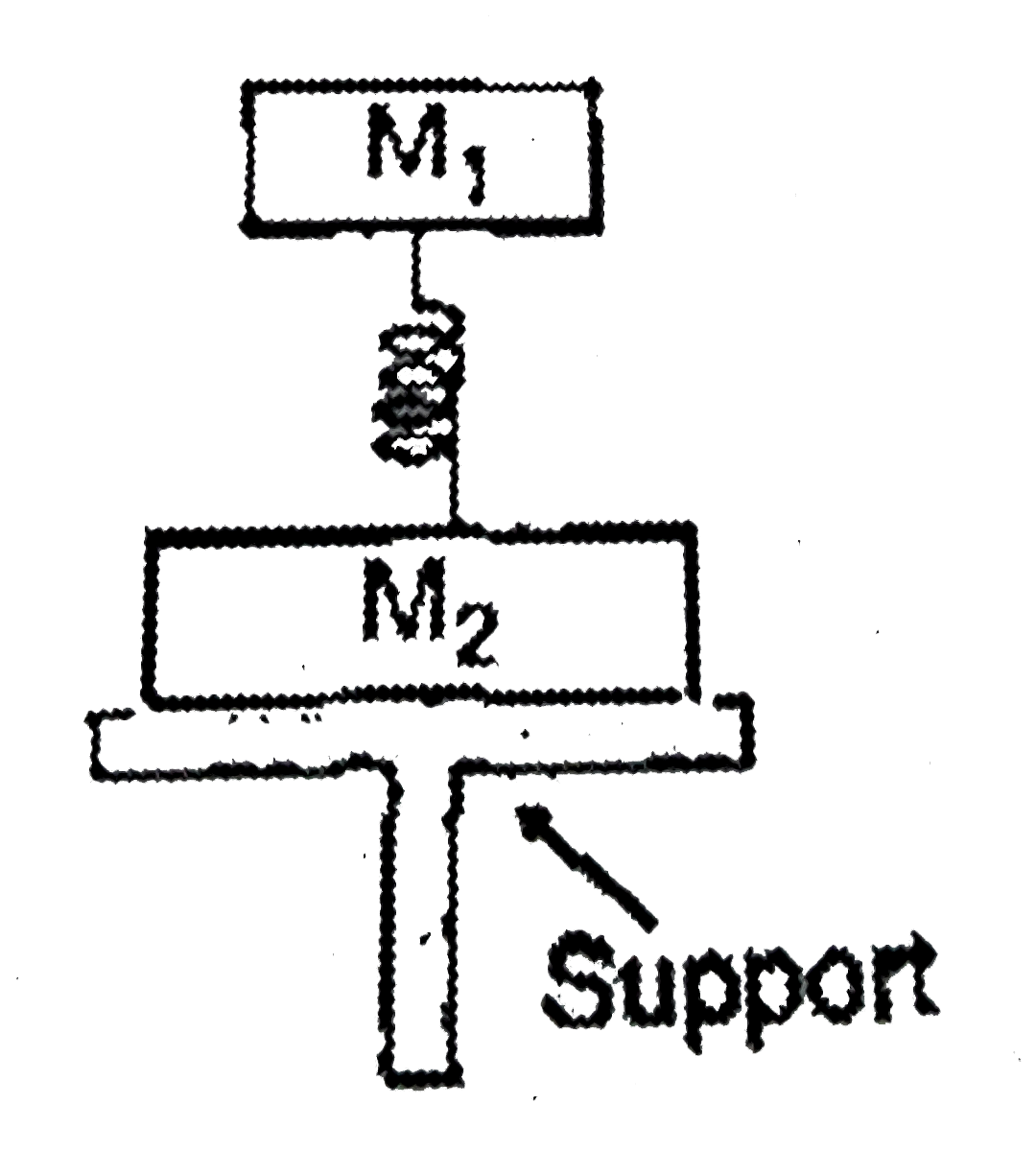 Aa1=ms−2,a2=2gms−2Ba1=g/2ms−2,a2=13gms−2Ca1=0,a2=32gms2Da1=23gms−2,a2=0
Aa1=ms−2,a2=2gms−2Ba1=g/2ms−2,a2=13gms−2Ca1=0,a2=32gms2Da1=23gms−2,a2=0Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of springAzeroBF(m1+m2)m1m2CFm1DFm1+m2Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
Which of the following statement is not true tn the watt of above system.ACentre of mass reference frame is an inertial frame.BKinetic energy of the system is minimum in centre of mass frame.CAt the instant of maximum deformation both the blocks are instantaneously at rest in centre of mass reference frameDAcceleration of centre of mass is constant in ground frame.
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA system consists of t wo identical masses A and B of mass m each connected to ends of a massless spring of force constant k as shown in figure.
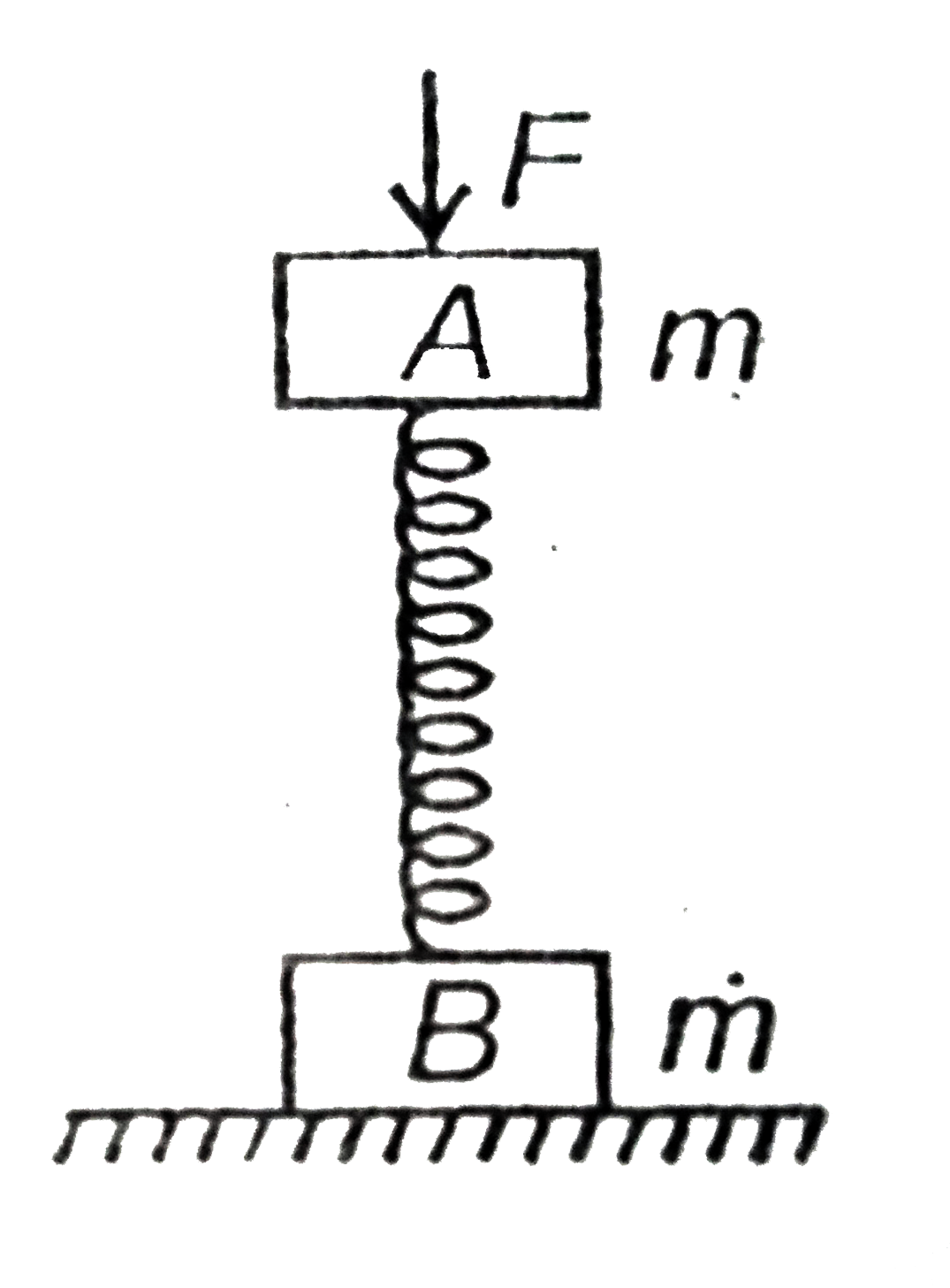
The minimum force F applied vertically downward on A, such that on its release, B will leave the floor.
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
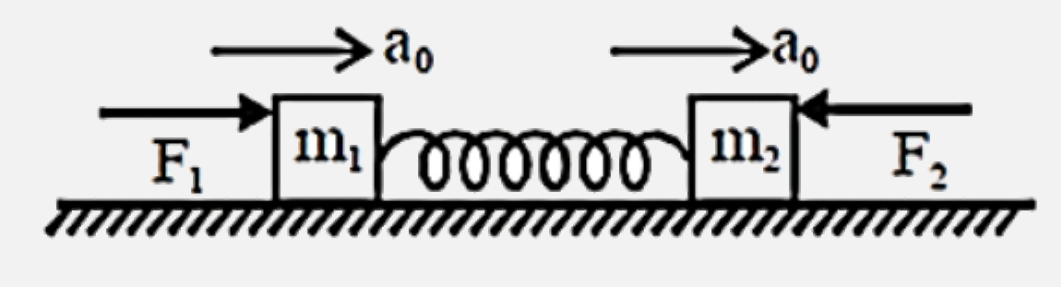
View SolutionThe system of two weights with masses M1 and M2 are connected with weightless spring as shown in fig. The system is resting on the support S. Find the acceleration of each of the weights just after the support S is quickly removed.
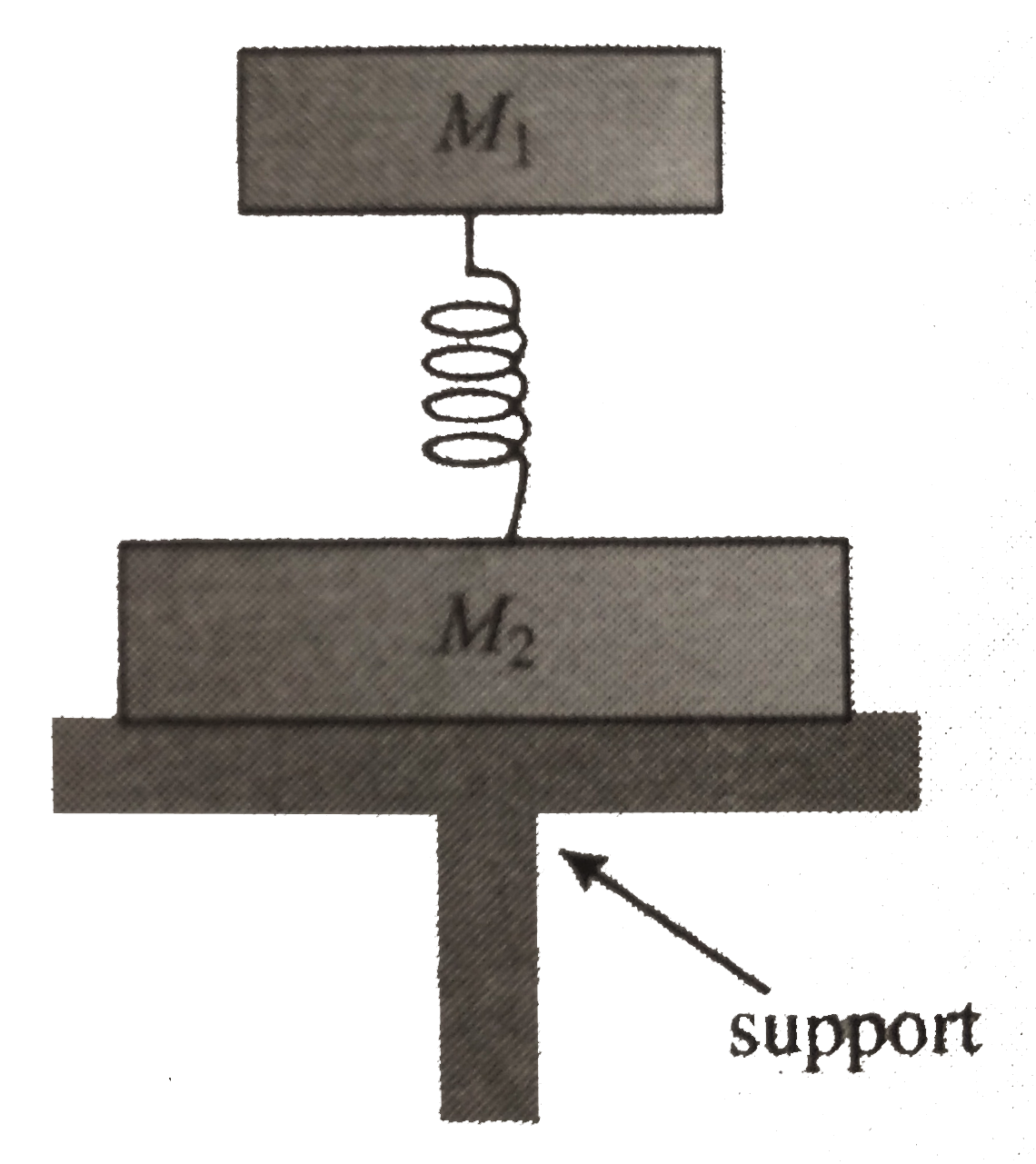
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
What is maximum elongation of spring.
View Solution
