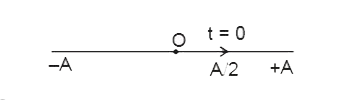
A particle starts from point $x = \frac{- \sqrt{3}}{2}$ A and move towards negative extreme as shown
(a) Find the equation of the SHM.
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.

Video Solution

Text Solution

Verified by Experts

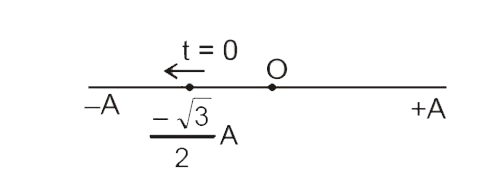
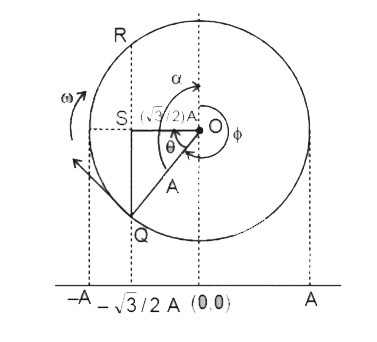
Figure shows the solution of the problem with the help of phasor Horizontal component of velocity at Q gives the required direction of velocity at t = 0.
In $Δ$ OSQ cos $θ = \frac{\sqrt{3} / 2 A}{A} = \frac{\sqrt{3}}{2} \Rightarrow θ = \frac{π}{6}$
Now $ϕ = \frac{3 n}{2} - \frac{π}{6} = \frac{8 π}{6} = \frac{4 π}{3}$
So , equation of SHM is
$x = A sin (ω t + \frac{4 π}{3})$
(b) Now to reach the particle at left extreme point it will travel angle $θ$ along the circle. So time taken.
$t = \frac{θ}{ω} = \frac{π}{6 ω} \Rightarrow t = \frac{T}{12}$ sec
(c) To reach the particle at mean position it will travel an angle $α = \frac{π}{2} + \frac{π}{6} = \frac{2 π}{3}$
So, time taken $= \frac{α}{ω} = \frac{T}{3}$ sec

Updated on:21/07/2023

A particles starts from point $x = - \frac{\sqrt{3}}{2} A$ and move towards negative extrene as shown . If the time period of oscillation is T , them

AThe equation of the SHM is $x = A sin (\frac{2 π}{T} + \frac{4 π}{3})$
BThe time taken by the particle tto go directly from its initial position to negative extreme is $\frac{T}{12}$
CThe time taken by the particle to reach at mean position is $\frac{T}{3}$
DThe equation of the SHM is $x = A sin (\frac{2 π}{T} + \frac{π}{3})$
A particle executes S.H.M with time period 12 s. The time taken by the particle to go directly from its mean position to half its amplitude.
A4 s
B3 s
C6 s
D1 s
A particle executes S.H.M. with a time period of 3s. The time taken by the particle to go directly from its mean position to half of its amplitude is-
A1s
B3/4 s
C1/3 s
D1/4 s