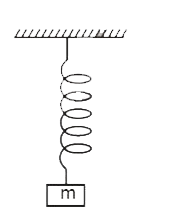
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.

Video Solution

Text Solution

Verified by Experts

The following steps are usually followed in this method :
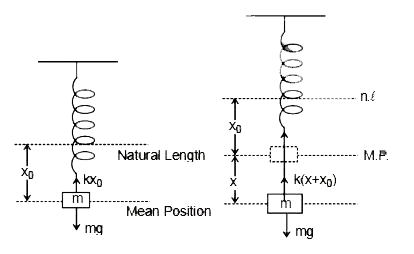
Step 1. Find the stable equillibrium position which is usually known as the mean position. Net force or torque on the particle at this position is zero. Potential energy is minimum. In our example initial position is the mean position.
Step 2. Write down the mean position force relation. In above figure at mean position
$k x_{0} = m g \dots (1)$
Step 3. Now displace the particle from its mean position by a small displacement x (in linear SHM) or angle $θ$ (in case of an angular SHM) as shown in figure.
Step 4. Write down the net force on the particle in the displaced position.
From the above figure.
$F_{net} = m g - k (x - x_{0}) \dots (2)$
Step 5. Now try to reduce this net force equation in the form of F = – kx (in linear S.H.M.) or $τ = - k θ$ (in angular SHM) using mean position force relation in step 2 or binomial theorem.
From eq. (2) $F_{net} = m g - k x = k x_{0}$
Usng eq (i) in above equation
$F_{net} = - k x \dots (3)$
Equation (3) shows that the net force acting towards mean position and is proportional to x, but in this S.H.M. constant $K_{S . H . M .}$ is replaced by spring constant k. So
$T = 2 π \sqrt{\frac{m}{K_{S . H . M .}}} = 2 π \sqrt{\frac{m}{k}}$

Updated on:21/07/2023