The system is in equilibrium and at rest. Now mass m1 is removed from m2 . Find the time period and amplitude of resultant motion. (Given : spring constant is K.)
Initial extension in the spring
x=m1+m2gK
Now, if we remove m1 . equillibrium position (E.P.) of m will be m2gKbelow natural length of spring. At the initial position, since velocity is zero i.e. it is the extreme position.
Hence Amplitude =m1gK
Time period =2π√m2K
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-A )8videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)8videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)14videos
SOUND WAVES
Similar Questions
The system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.
 View Solution
View SolutionA horizontal spring block system of mass M executes simple haormonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m1 and m2 are suspended w together by a light spring of spring constant k as shown in figure. When the system is in equilibrium, the mass m1 is removed without disturbing the system. As a result of this removal, mass m2 performs simple harmonic motion. For this situation mark the correct statement(s).
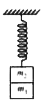 AThe amplitude of osciallation is m1gkBThe amplitude of oscillations is (m1+m2)gkCThe system oscillates with angular frequency √km2DThe system oscillates with angular frequency √km1+m2
AThe amplitude of osciallation is m1gkBThe amplitude of oscillations is (m1+m2)gkCThe system oscillates with angular frequency √km2DThe system oscillates with angular frequency √km1+m2 - Question 2 - Select One
A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
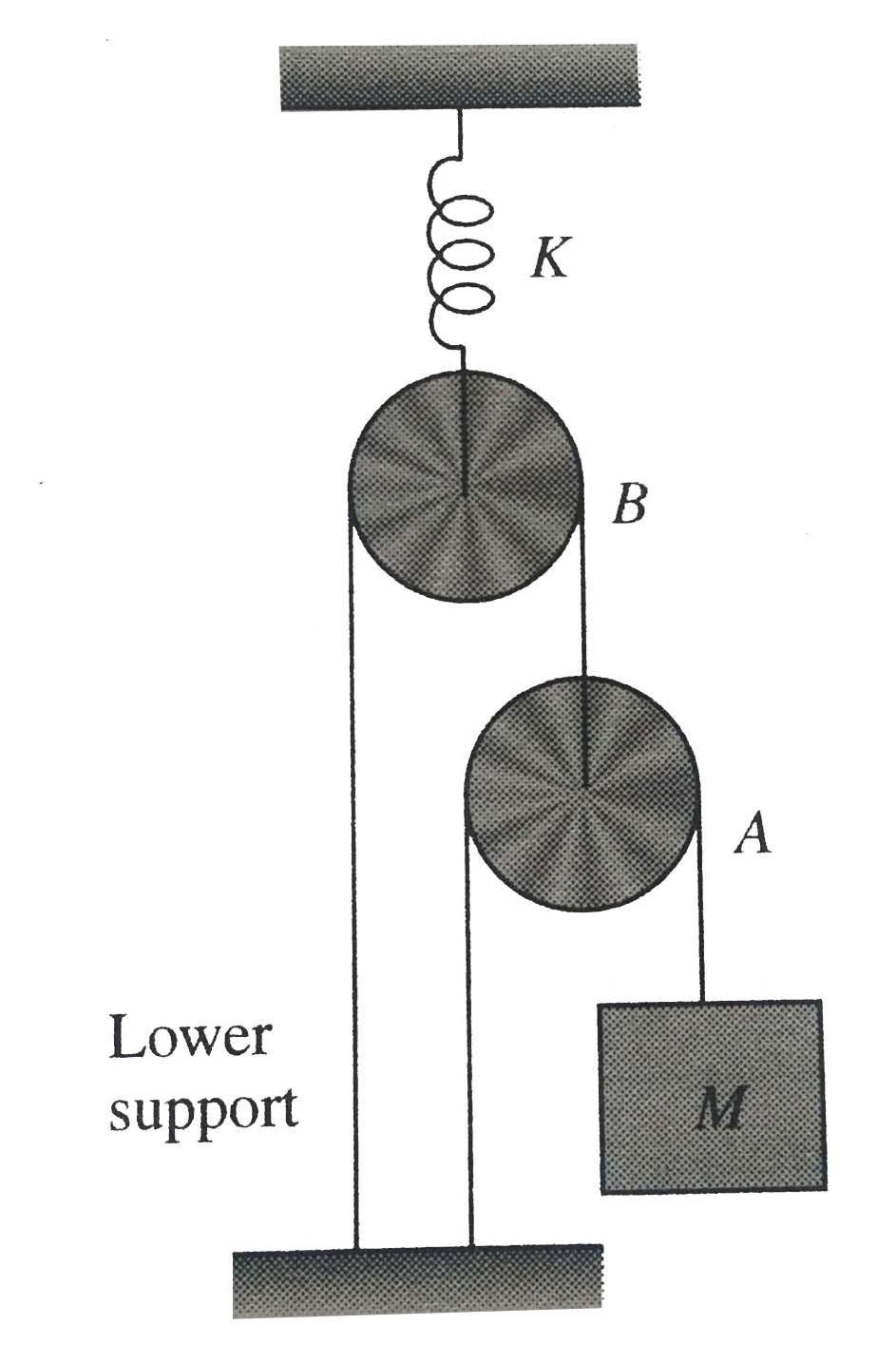
The extension produced in the spring is given byA4Mg/KBMg/KC2Mg/KD3Mg/K - Question 3 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
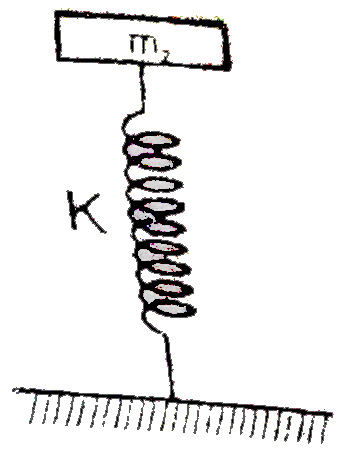 View Solution
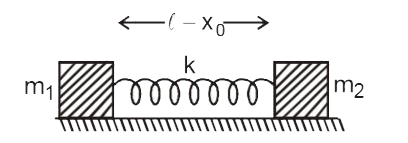
View SolutionTwo blocks of mass m1 and m2 are connected with a spring of natural length l and spring constant k. The system is lying on a smooth horizontal surface. Initially spring is compressed by x0 as shown in figure. Show that the two blocks will perform SHM about their equilibrium position. Also (a) find the time period, (b) find amplitude of each block and (c) length of spring as a function of time.
 View Solution
View SolutionA block of mass M is lying on a frictionless horizontal surface and it connected to a spring of spring constant k, whose other end is fixed to a wall, system executes simple harmonic motion of amplitude A0, when the block is passing through its equilibrium positions, an object of mass m is put on it and the two move together with a new time period T and amplitude A. Find the value of T and A in terms of given constants.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 View Solution
View Solution

