Two springs of the same material but of length L and 2L are suspended with masses M and 2M attached at their lower ends. Their time periods when they are allowed to oscillate will be in the ratio

A

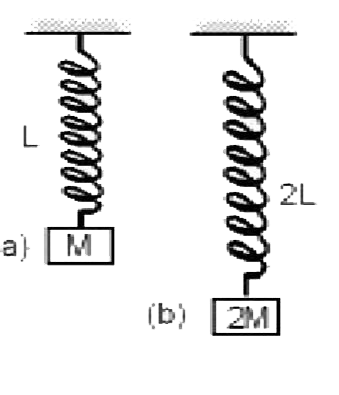
$1 : 2$

B

$2 : 1$

C

$1 : 4$

D

$4 : 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

|

Answer

Step by step video & image solution for Two springs of the same material but of length L and 2L are suspended with masses M and 2M attached at their lower ends. Their time periods when they are allowed to oscillate will be in the ratio by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
A $2 π \sqrt{\frac{(M + m) l}{M g}}$
B $2 π \sqrt{\frac{m l}{M g}}$
C $2 π \sqrt{L / g}$
D $2 π \sqrt{\frac{M l}{(m + M) g}}$
Question 2 - Select One or More
A metal wire of length $L$ is suspended vertically from a rigid support. When a bob of mass $M$ is attached to the lower end of wire, the elongation of the wire is $l :$
AThe loss in gravitational potential energy of mass $M$ is $M g l$ .
BThe elastic potential energy stored in the wire is $M g l$
CThe elastic potential energy stored in the wire is $\frac{1}{2} M g l$
DHeat produced is loss of mechanical energy of system is $\frac{1}{2} M g l$
Question 3 - Select One
The young modulii of two springs of equal length and equal cross sectional areas are in the ratio 2:3 both the springs are suspended and loaded with the same mass . When springs are stretched and released , the time period of oscillation of the two springs is in the ratio of
A3:2
B2:3
C $\sqrt{3} : \sqrt{2}$
D $\sqrt{2} : \sqrt{3}$

MOTION-SIMPLE HARONIC MOTION -EXERCISE -1 ( SECTION-D ) ( Combination of springs)

Home
Ask Doubt
Profile