In the figure, the block of mass m, attached to the spring of stiffness k is in contact with the complete elastic wall, and the compression in the spring is 'e'. The spring is compressed further by 'e' by displacing the block towards left and is then released. if the collision between the block and the wall is completely elastic then the time priod of oscillations of the block will be-

2π3√mk
2π√mk
π3√mk
π6√mk
The correct Answer is:A
Step by step video & image solution for In the figure, the block of mass m, attached to the spring of stiffness k is in contact with the complete elastic wall, and the compression in the spring is 'e'. The spring is compressed further by 'e' by displacing the block towards left and is then released. if the collision between the block and the wall is completely elastic then the time priod of oscillations of the block will be- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - D ) ( Combination of springs )5videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - E,F ) ( Angu lar shm & s implependulum )1videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - B ) ( Time per iod and angu larfrequency in SHM )7videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)14videos
SOUND WAVES
Similar Questions
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
 View Solution
View SolutionA block of mass 100g attached to a spring ofstiffness 100N/Mis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collation with the wall is elastic then find the time period of oscillations.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk - Question 2 - Select One
A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
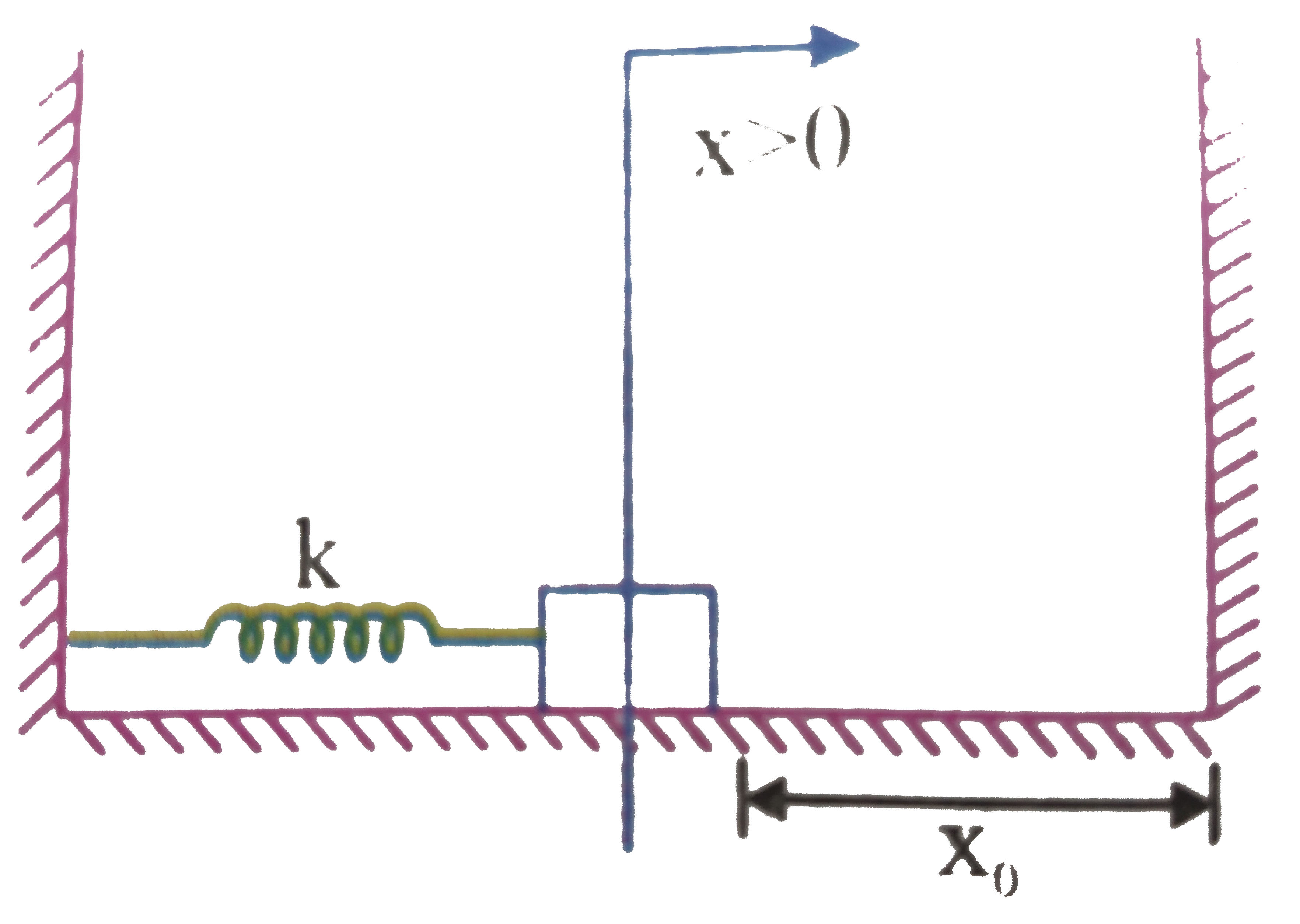
Find the time period of motion of the block:A2π3√mkB4π3√mkC3π2√mkDπ2√mk - Question 3 - Select One
A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these
Figure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.
 View Solution
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
 View Solution
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionThe block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?
 View Solution
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
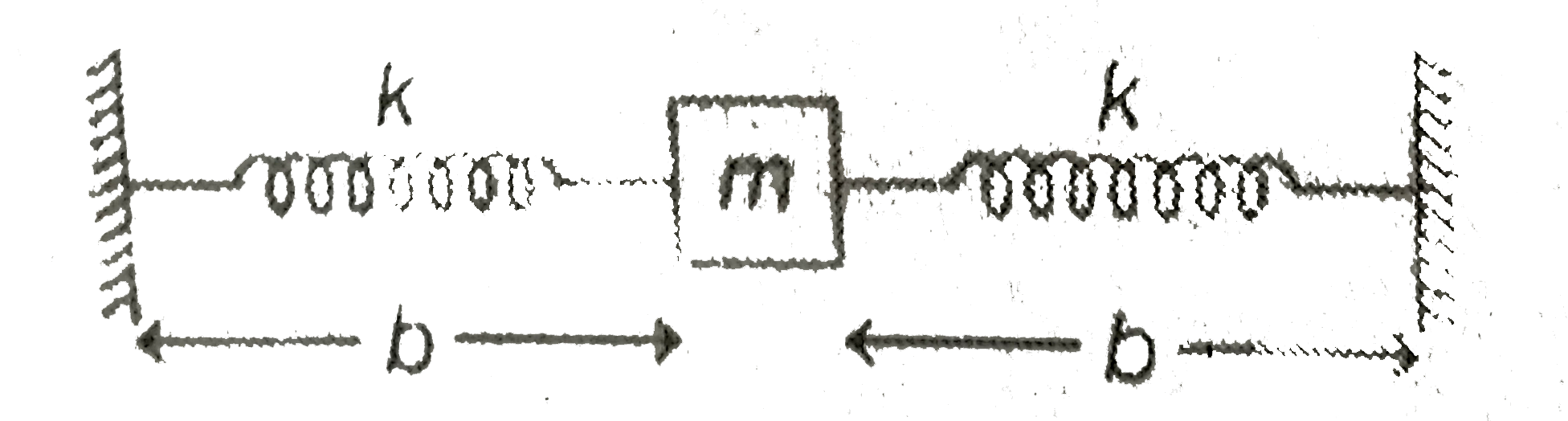 View Solution
View Solution

