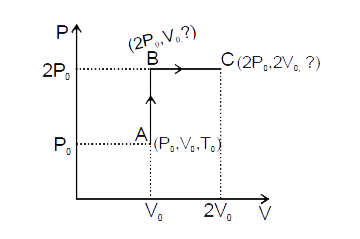
Find out the values of co-ordinates at point A, B, C in terms of pressure , volume and temperature and draw curve.
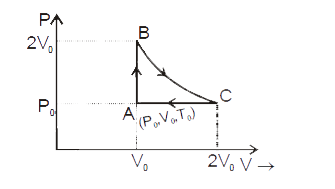
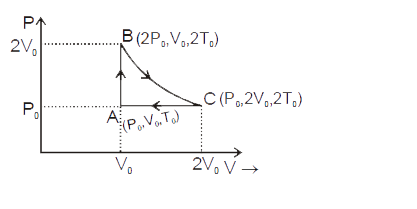
A→B Volume Const (Isochoric) P1T1=P2T2
B→C Temp. Const (Isothermal) P1V1=P2V2
C→A Pressure Const (Isobaric) V1T1=V2T2
(##MOT_CON_JEE_PHY_C16_SLV_003_S02.png" width="80%">
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-140videos
HEAT-2
- BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-2 (LEVEL-I)24videos
HEAT-2
- BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-B19videos
HEAT TRANSFER & THERMAL EXPANSION
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM7videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Different curves of volume vs temperature at constant pressure are called
AIsothermBIsobarCIsochoreDIsotope
_S01_021_Q01.png)
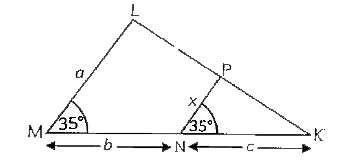
Find out pressure at points A and B also find angle θView SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionEvaluate the value of x in terms of a, b and c.
 View Solution
View SolutionTwo vessels A and B of equal volume (V0) are connected by a narrow tube which can be closed by a value. The vessels are fitted with piston which can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (CpCv=γ) at atomspheric pressures(P0) and atmoshpeheric temperature (T0). The walls of the vessels A are diathermic and those of B are adiabatic. The value is now closed and the pistons are slowly pulled out to increase the volumes of the of the vessels to dobuled the original value.(a) Find the temperatures and pressures in the two vessels. (b) The value is now opened for sufficeint time so that the gases acquire a common tempertures and pressures . Find the new values of the temperatuere and the pressures.
View SolutionFind the co -ordinates of the mid point of the join of the points A(3,5,7) and B(-3,-3,1)
View Solutionxa+yb+zc=1 intersects the co-ordinate axes at points A ,B and C respectively. If ΔPQR has mid-points A,B and C then find area of ΔPQR
View SolutionA curve is such that the ratio of the subnomal at any point to the sum of its co-ordinates is equal tothe ratio of the ordinate of this point to its abscissa. If the curve passes through M(1,0), then possible equation of the curve is(are)
View Solution