Three rods of equal of length are joined to from an equilateral triangle ABC. $D$ is the midpoint of AB. The coefficient of linear expansion is $α_{1}$ for AB and $α_{2}$ for $A C$ and $B C$ . If the distance $D C$ remains constant for small changes in temperature,

$α_{1} = α_{2}$

$α_{1} = 2 α_{2}$

$α_{1} = 4 α_{2}$

$α_{1} = \frac{1}{2} α_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video & image solution for Three rods of equal of length are joined to from an equilateral triangle ABC. D is the midpoint of AB. The coefficient of linear expansion is alpha_(1) for AB and alpha_(2) for AC and BC . If the distance DC remains constant for small changes in temperature, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELASTICITY AND THERMAL EXPANSION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
An equilateral triangle $A B C$ is formed by joining three rods of equal length and $D$ is the mid-point of $A B$ . The coefficient of linear expansion for $A B$ is $α_{1}$ and for $A C$ and $B C$ is $α_{2}$ . The relation between $α_{1}$ and $α_{2}$ , if distance $D C$ remains constant for small changes in temperture is

A $α_{1} = α_{2}$
B $α_{1} = 4 α_{2}$
C $α_{2} = 4 α_{1}$
D $α_{1} = \frac{1}{2} α_{2}$
Question 2 - Select One
Two rods , one of aluminium and the other made of steel, having initial length $l_{1}$ and $l_{2}$ are connected together to from a sinlge rod of length $l_{1} + l_{2}$ . The coefficient of linear expansion for aluminium and steel are $α_{a}$ and $α_{s}$ for $A C$ and $B C$ . If the distance $D C$ remains constant for small changes in temperature,
A $\frac{α_{s}}{α_{a}}$
B $\frac{α_{a}}{α_{s}}$
C $\frac{α_{s}}{(α_{a} + α_{s})}$
D $\frac{α_{a}}{(α_{a} + α_{s})}$
Question 3 - Select One
Three rods of equal l are joined to from an equilateral triangle PQR.O is the mid-point of PQ. Distance OR remains same for small change in temperature. Coefficient of linear expansion for PR and RQ is same i.e., $α_{2}$ but for PQ is $α_{1^{.}}^{.}$ Then

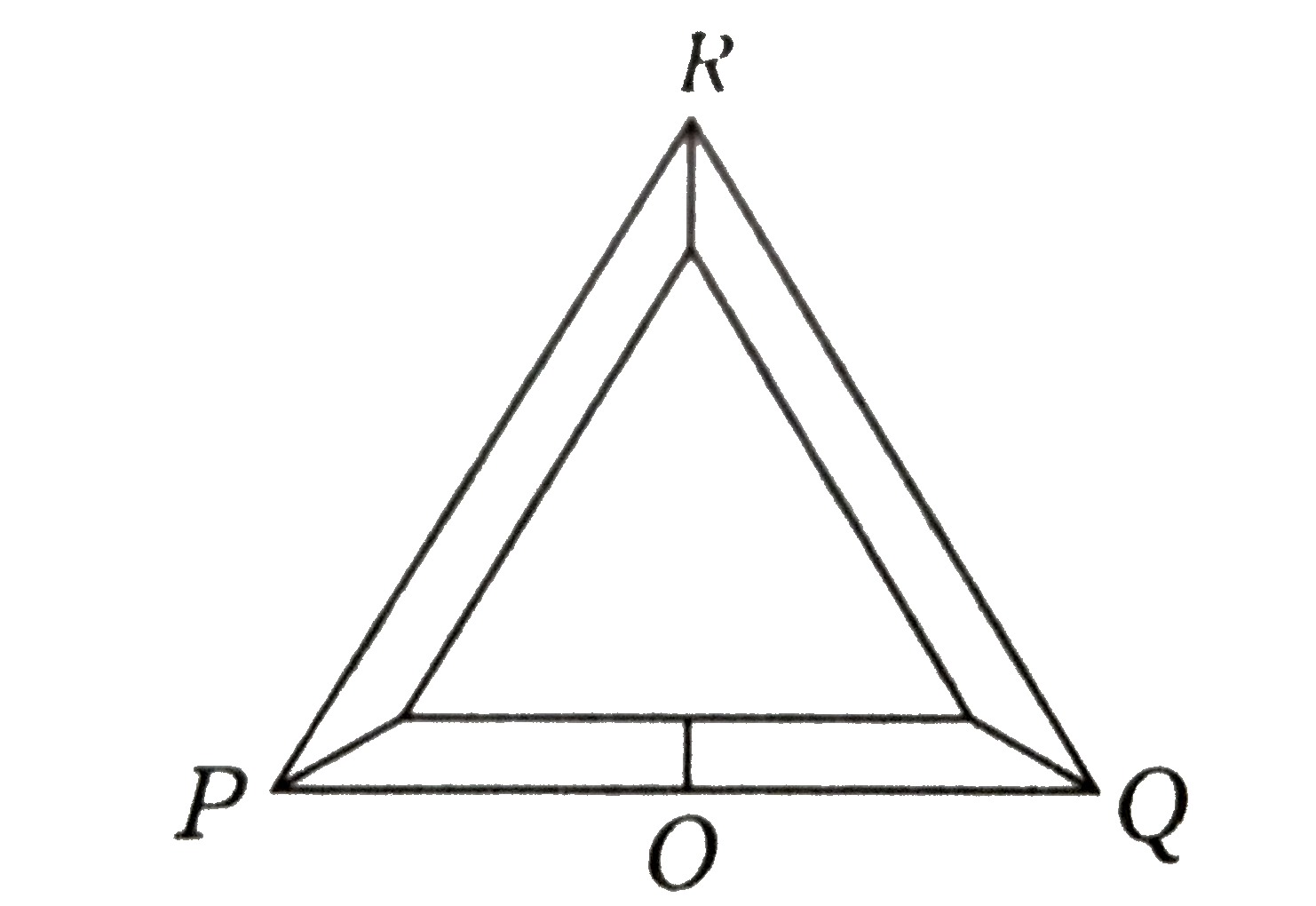A $α_{2} = 3 α_{1}$
B $α_{2} = 4 α_{1}$
C $α_{1} = 3 α_{2}$
D $α_{1} = 4 α_{2}$

MOTION-ELASTICITY AND THERMAL EXPANSION-Exercise -1 (Section B - Thermal Stress, Hookes Law)

Home
Ask Doubt
Profile

Three rods of equal of length are joined to from an equilateral triangle ABC. D is the midpoint of AB. The coefficient of linear expansion is α1 for AB and α2 for AC and BC . If the distance DC remains constant for small changes in temperature,

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

An equilateral triangle ABC is formed by joining three rods of equal length and D is the mid-point of AB. The coefficient of linear expansion for AB is α1 and for AC and BC is α2. The relation between α1 and α2, if distance DC remains constant for small changes in temperture is

Three rods of equal l are joined to from an equilateral triangle PQR.O is the mid-point of PQ. Distance OR remains same for small change in temperature. Coefficient of linear expansion for PR and RQ is same i.e., α2 but for PQ is α1. Then

MOTION-ELASTICITY AND THERMAL EXPANSION-Exercise -1 (Section B - Thermal Stress, Hookes Law)

Three rods of equal of length are joined to from an equilateral triangle ABC. $D$ is the midpoint of AB. The coefficient of linear expansion is $α_{1}$ for AB and $α_{2}$ for $A C$ and $B C$ . If the distance $D C$ remains constant for small changes in temperature,

Three rods of equal l are joined to from an equilateral triangle PQR.O is the mid-point of PQ. Distance OR remains same for small change in temperature. Coefficient of linear expansion for PR and RQ is same i.e., $α_{2}$ but for PQ is $α_{1^{.}}^{.}$ Then