A uniform rod rotating in gravity free region with certain constant angular velocity. The variation of tensile stress with distance x from axis of rotation is best represented by which of the following graphs.

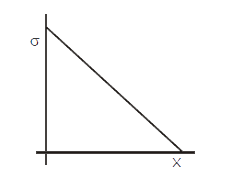
The correct Answer is:A
To solve the problem of determining the variation of tensile stress with distance x from the axis of rotation in a uniform rod rotating in a gravity-free region, we can follow these steps:
Step 1: Understand the System
We have a uniform rod rotating about an axis with a constant angular velocity ω. We need to find how the tensile stress varies with distance x from the axis of rotation.
Step 2: Define the Differential Element
Consider a small element of the rod at a distance x from the axis of rotation. Let the length of this element be dx and its mass be dm.
Step 3: Identify Forces Acting on the Element
The forces acting on this differential element include:
- Tension T at one end of the element.
- Tension T+dT at the other end of the element.
- Centrifugal force acting outward, given by Fc=dm⋅ω2⋅x.
Step 4: Set Up the Force Balance Equation
For the element to be in equilibrium, the net force must be zero. Thus, we can write:
T+dT−T−dm⋅ω2⋅x=0
This simplifies to:
dT=dm⋅ω2⋅x
Step 5: Express dm in Terms of dx
Since the rod is uniform, the mass per unit length λ is constant. Therefore, we can express dm as:
dm=λ⋅dx
where λ=mL (mass per unit length).
Step 6: Substitute dm into the Equation
Substituting dm into the force balance equation gives:
dT=λ⋅dx⋅ω2⋅x
Step 7: Integrate to Find Tension
Integrating both sides, we have:
∫dT=∫λ⋅ω2⋅xdx
This results in:
T=λ⋅ω22x2+C
where C is the constant of integration.
Step 8: Determine the Constant of Integration
At the free end of the rod (where x=L), the tension T is zero. Thus:
0=λ⋅ω22L2+C⟹C=−λ⋅ω22L2
Substituting back, we get:
T=λ⋅ω22(x2−L2)
Step 9: Relate Tension to Stress
The tensile stress σ at a distance x is given by:
σ=TA
where A is the cross-sectional area of the rod. Thus:
σ=λ⋅ω22A(L2−x2)
Step 10: Analyze the Resulting Equation
The equation for stress can be rewritten as:
σ=k(L2−x2)
where k=λ⋅ω22A is a constant. This is a downward-opening parabola.
Conclusion
The variation of tensile stress with distance x from the axis of rotation is best represented by a downward-opening parabola.
We have a uniform rod rotating about an axis with a constant angular velocity ω. We need to find how the tensile stress varies with distance x from the axis of rotation.
Consider a small element of the rod at a distance x from the axis of rotation. Let the length of this element be dx and its mass be dm.
The forces acting on this differential element include:
- Tension T at one end of the element.
- Tension T+dT at the other end of the element.
- Centrifugal force acting outward, given by Fc=dm⋅ω2⋅x.
For the element to be in equilibrium, the net force must be zero. Thus, we can write:
T+dT−T−dm⋅ω2⋅x=0
This simplifies to:
dT=dm⋅ω2⋅x
Since the rod is uniform, the mass per unit length λ is constant. Therefore, we can express dm as:
dm=λ⋅dx
where λ=mL (mass per unit length).
Substituting dm into the force balance equation gives:
dT=λ⋅dx⋅ω2⋅x
Integrating both sides, we have:
∫dT=∫λ⋅ω2⋅xdx
This results in:
T=λ⋅ω22x2+C
where C is the constant of integration.
At the free end of the rod (where x=L), the tension T is zero. Thus:
0=λ⋅ω22L2+C⟹C=−λ⋅ω22L2
Substituting back, we get:
T=λ⋅ω22(x2−L2)
The tensile stress σ at a distance x is given by:
σ=TA
where A is the cross-sectional area of the rod. Thus:
σ=λ⋅ω22A(L2−x2)
The equation for stress can be rewritten as:
σ=k(L2−x2)
where k=λ⋅ω22A is a constant. This is a downward-opening parabola.
The variation of tensile stress with distance x from the axis of rotation is best represented by a downward-opening parabola.
Topper's Solved these Questions
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 2 (Level-I) (Section C - Youngs Modulus, Poissions Ratio)
2 Videos
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 2 (Level-I) (Section D - Thermal Expansion (Solid , Liquids & Gas) & types, Applications (Ex Bimetallic strip etc))
2 Videos
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 2 (Level-I) (Section A - Stress & types, Strain & types + Types of Modulus + Energy Problems + Graphs)
3 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
Similar Questions
A copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
View SolutionA circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
View Solution
Knowledge Check
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A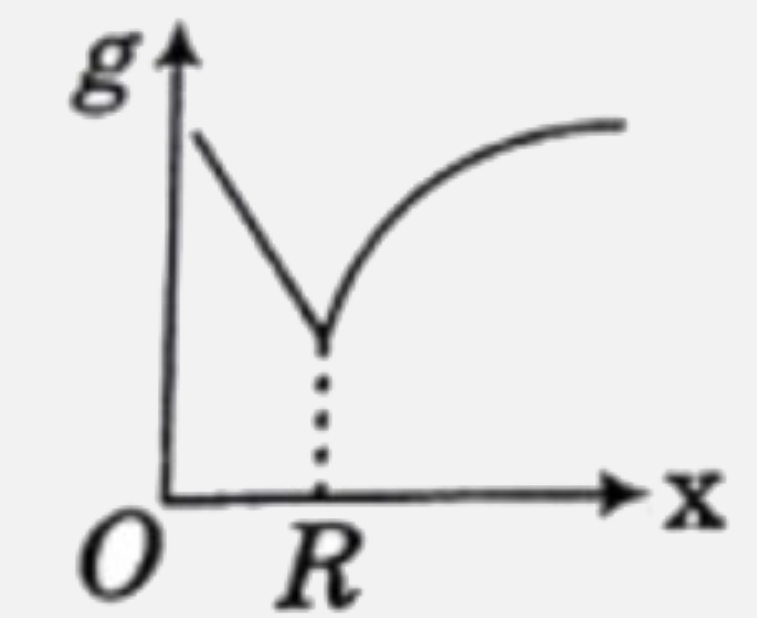 B
B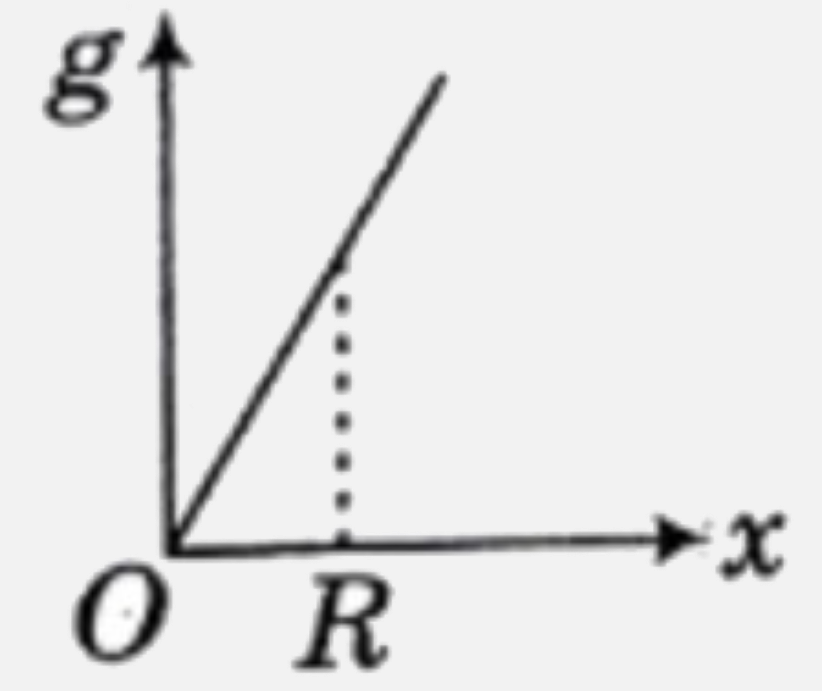 C
C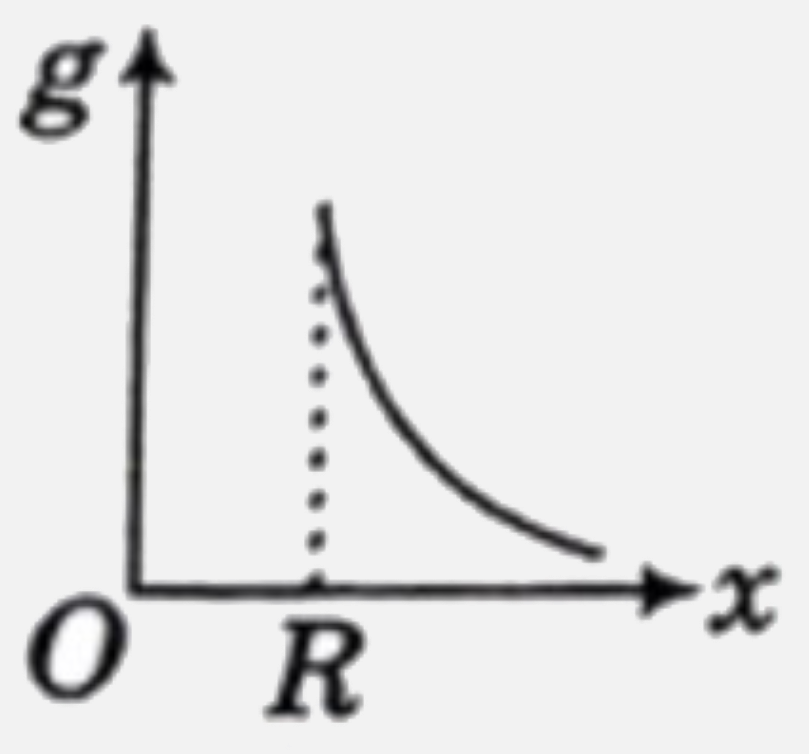 D
D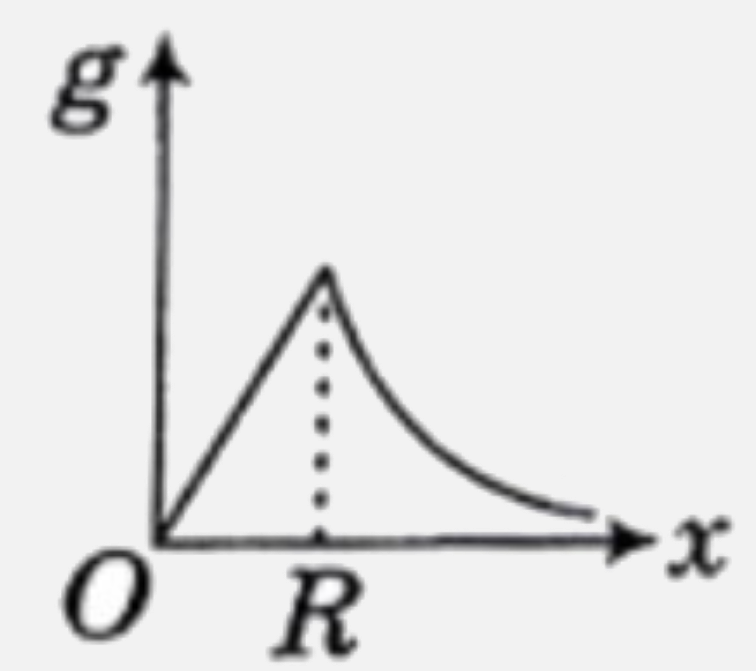
A wheel rotates with a constant angular velocity of 600 rpm. What is the angle through which the wheel rotates in 1s?
A5π radB20πradC15π radD10π radA wheel rotates with a constant angular velocity of 300 rpm. The angle through which the wheel rotates in 1 s is.
Aπ radB5π radC10π radD20π rad
The graph that represents variation of g at the equator with square of angular velocity of rotation of earth is
View SolutionA uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis, then which of the following graphs depicts it most closely ?
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA circular plate is rotating about its own axis at an angular velocity 100 revolutions per minute. The linear velocity of a particle P of plate at a distance 4.2cm from axis of rotation is
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View Solution
