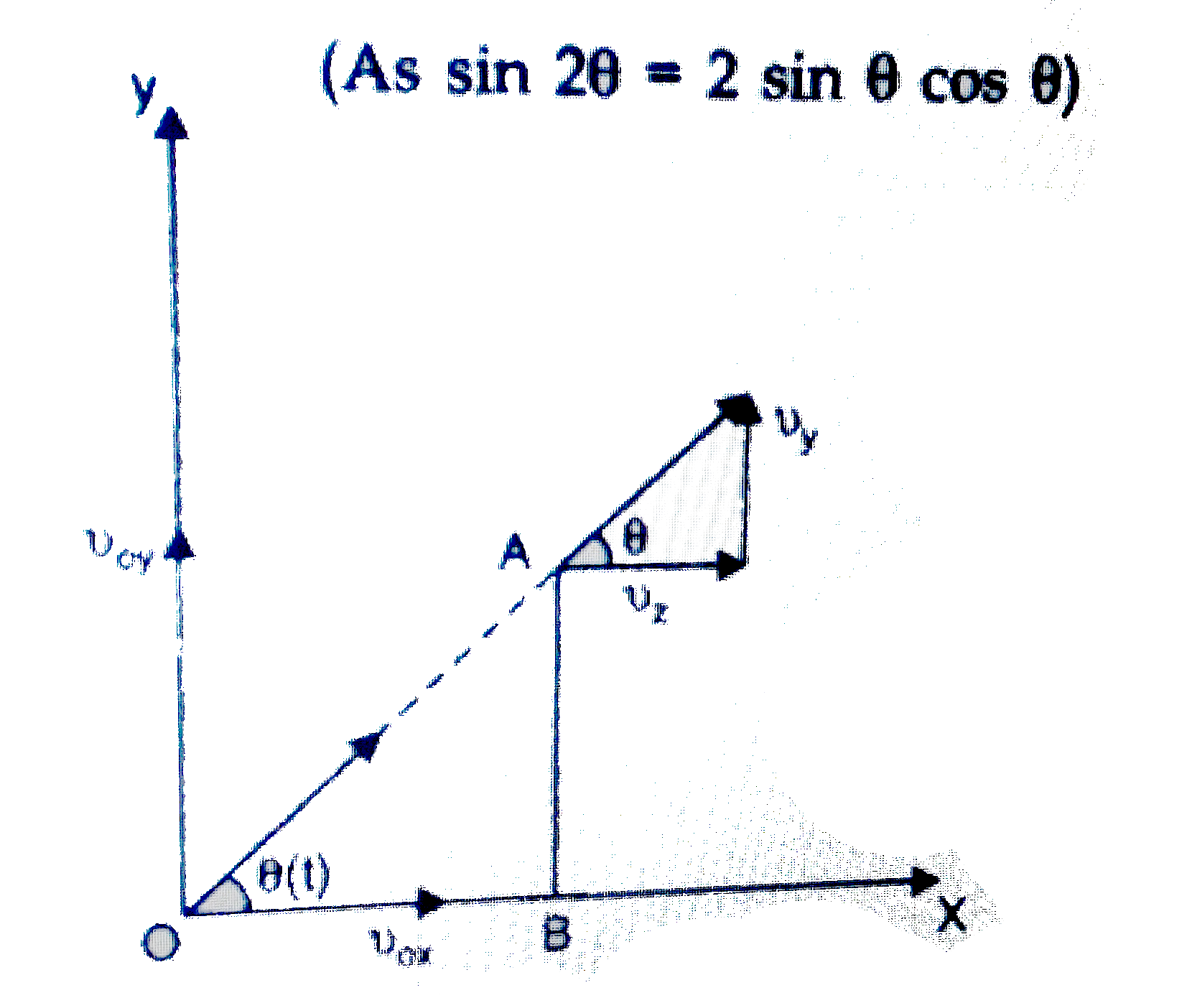
Show that for a projectile the angle between the velocity and the x-axis as function of time is given
by $θ_{t} = \tan^{- 1} (\frac{v_{0 y} - g t}{v_{o x}})$
(b) Shows that the projection angle $θ_{0}$ for a projectile launched from the origin is given by $θ_{t} = \tan^{- 1} (\frac{4 h_{m}}{R})$
where the symbols have their usual meanings.

Video Solution

Text Solution

Verified by Experts

a) Let the principle be fired at an angle $θ$ with x-axis. As $θ$ depends on t, $θ$ (t), at any instant
$\tan θ (t) = \frac{v_{y}}{v_{x}} = \frac{v_{o y} - >}{v_{e x}}$
b) Since, $h_{max} = \frac{u^{2} \sin^{2} θ}{2 g}$
and $R = \frac{u^{2} \sin 2 θ}{g}$
$\Rightarrow \frac{h_{max}}{R} = \frac{u^{2} \sin^{2} θ / 2 g}{u^{2} \sin 2 θ / g} = \frac{\tan θ}{4}$ (As $\sin 2 θ = 2 \sin θ \cos θ)$
$\Rightarrow \frac{\tan θ}{4} = \frac{h_{max}}{R}$
or $\tan θ = (4 \frac{h_{max}}{R}$
or $θ = \tan^{- 1} (\frac{4 h_{max}}{R})$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the angle between the lines $\sqrt{3} y - x + 4 = 0$ and $x + y - 6 = 0$ is $θ$ , then tan $θ$ is equal to.
A $\sqrt{3} + 1$
B $\sqrt{3} - 1$
C $2 + \sqrt{3}$
D $3 + \sqrt{2}$
Question 2 - Select One
The angle between the two lines $1 x + m y + n = 0$ and $1' x + m' y + n' = 0$ is given by ${tan}^{- 1} θ$ . What $θ$ equal to ?
A $∣ ∣ ∣ \frac{l m' - l' m}{l l' - m m'} ∣ ∣ ∣$
B $∣ ∣ ∣ \frac{l m' + l' m}{l l' + m m'} ∣ ∣ ∣$
C $∣ ∣ ∣ \frac{l m' - l' m}{l l' + m m'} ∣ ∣ ∣$
D $∣ ∣ ∣ \frac{l m' + l' m}{l l' - m m'} ∣ ∣ ∣$
Question 3 - Select One
A projectile is fired from the origin with a velocity $v_{0}$ at an angle $θ$ with x-axis. The speed of the projectile at an altitude $h$ is .
A $v_{0} cos θ$
B $\sqrt{v_{0}^{2} - 2 g h}$
C $\sqrt{v_{0}^{2} {sin}^{2} θ - 2 g h}$
DNone of these

NCERT-MOTION IN A PLANE -EXERCISE

Home
Ask Doubt
Profile