Uranium has two isotopes of masses 235 and 238 units. If both are present in uranium hexa fluoride gas, which would have the larger average speed ? If atomic mass of fluorine is 19 units, estimate the percentage difference in speed at any temperature.
Answer At a fixed temperature the average energy = lt m ltv2 gt is constant. So smaller the mass of the molecule, faster will be the speed. The ratio of speeds is inversely proportional to the square root of the ratio of the masses. The masses are 349 and 352 units. So
v349/v352=(352/349)1/2=1.0044.
Hence difference ΔVV=0.44% [235U is the isotope needed for nuclear fission. To separate it from the more abundant isotope 235U , the mixture is surrounded by a porous cylinder. The porous cylinder must be thick and narrow, so that the molecule wanders through individually, colliding with the walls of the long pore. The faster molecule will leak out more than the slower one and so there is more of the lighter molecule (enrichment) outside the porous cylinder (Fig. 13.5). The method is not very efficient and has to be repeated several times for sufficient enrichment.].
Topper's Solved these Questions
Similar Questions
Chlorine has two isotopes of atomic mass units 34.97uand36.97u. The relative abundances of these two isotopes are 0.735and0.245 respectively. Find out the average atomic mass of chlorine.
View SolutionChlorine has two isotopes of atomic mass units 34.97uand36.97u. The relative abundances of these two isotopes are 0.735and0.245 respectively. Find out the average atomic mass of chlorine.
View Solution
Knowledge Check
Uranium. has two isotopes of masses 235 and 238 units. If both of them are present in Uranium hexafluoride gas, find the percentage ratio of difference in rms velocities of two isotopes to the rms velocity of heavier isotope.
A1.64B0.064C0.64D6.4Chlorine has two isotopes having masses 34.98 u and 36.98 u with relative abundance of 75.4% and 24.6%,respectively. The average atomic mass of chlorine is
A34.98B36.98C35.47D35The speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
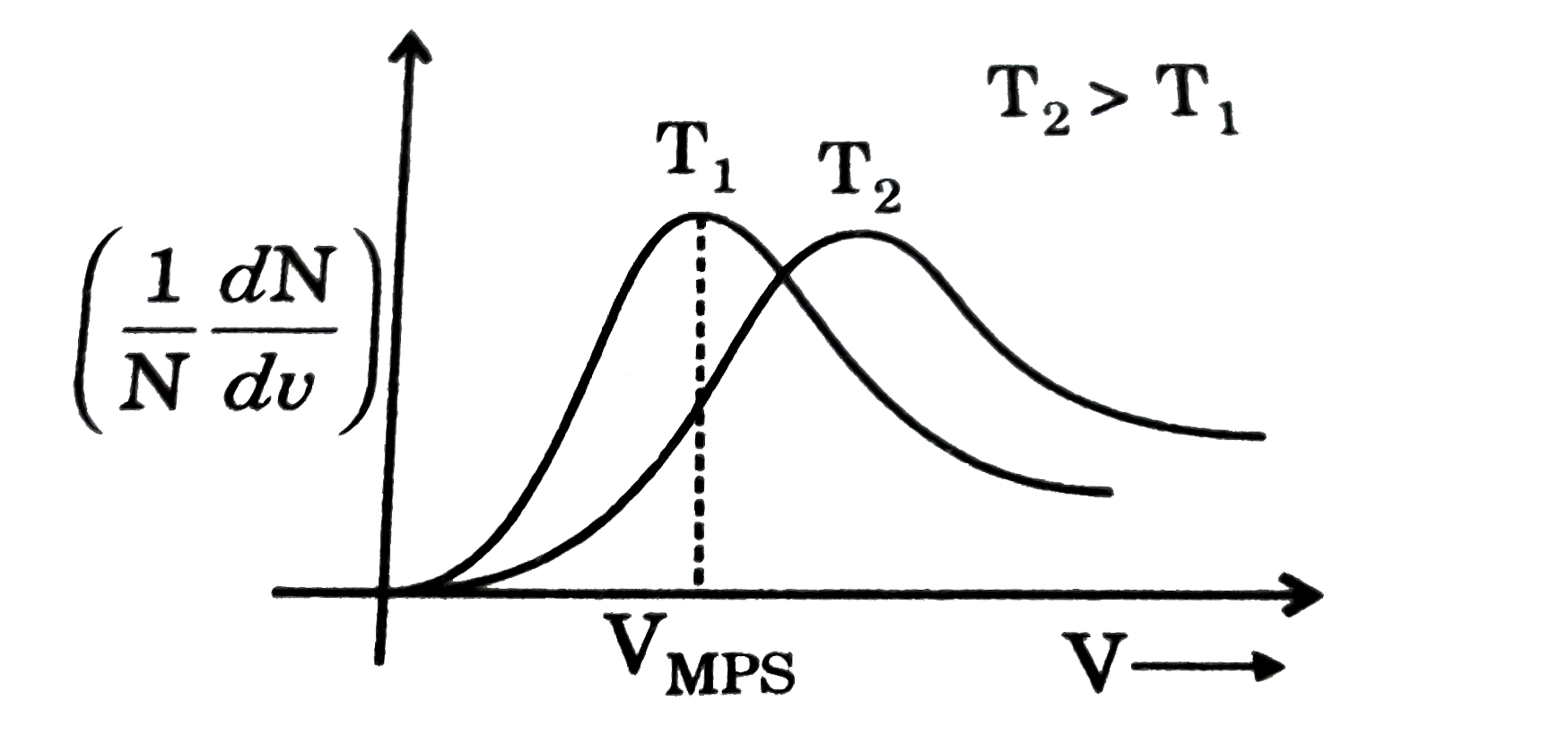
For the above graph, drawn for two different samples of gases at two different temperature T1andT2. Which of the following statements is necessarily true?AIfT2<T1,MAis necessarily greater thanMBBIfT1>T2,MBis necessarily greater thanMACT2MB<T1MADNothing can be predicted
If the average atomic mass fo chlorine is 35.5 then find the percentage abundance of the two isotopes of chlorine which have the mass number 35 and 37.
View SolutionIf the average atomic mass fo chlorine is 35.5 then find the percentage abundance of the two isotopes of chlorine which have the mass number 35 and 37.
View SolutionMass number of two isotopes of an element differ by 2 unit (A and A + 2) . Average atomic mass is 0.5 more than the lower mass number. What could be the ratio of the two isotopes.
View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
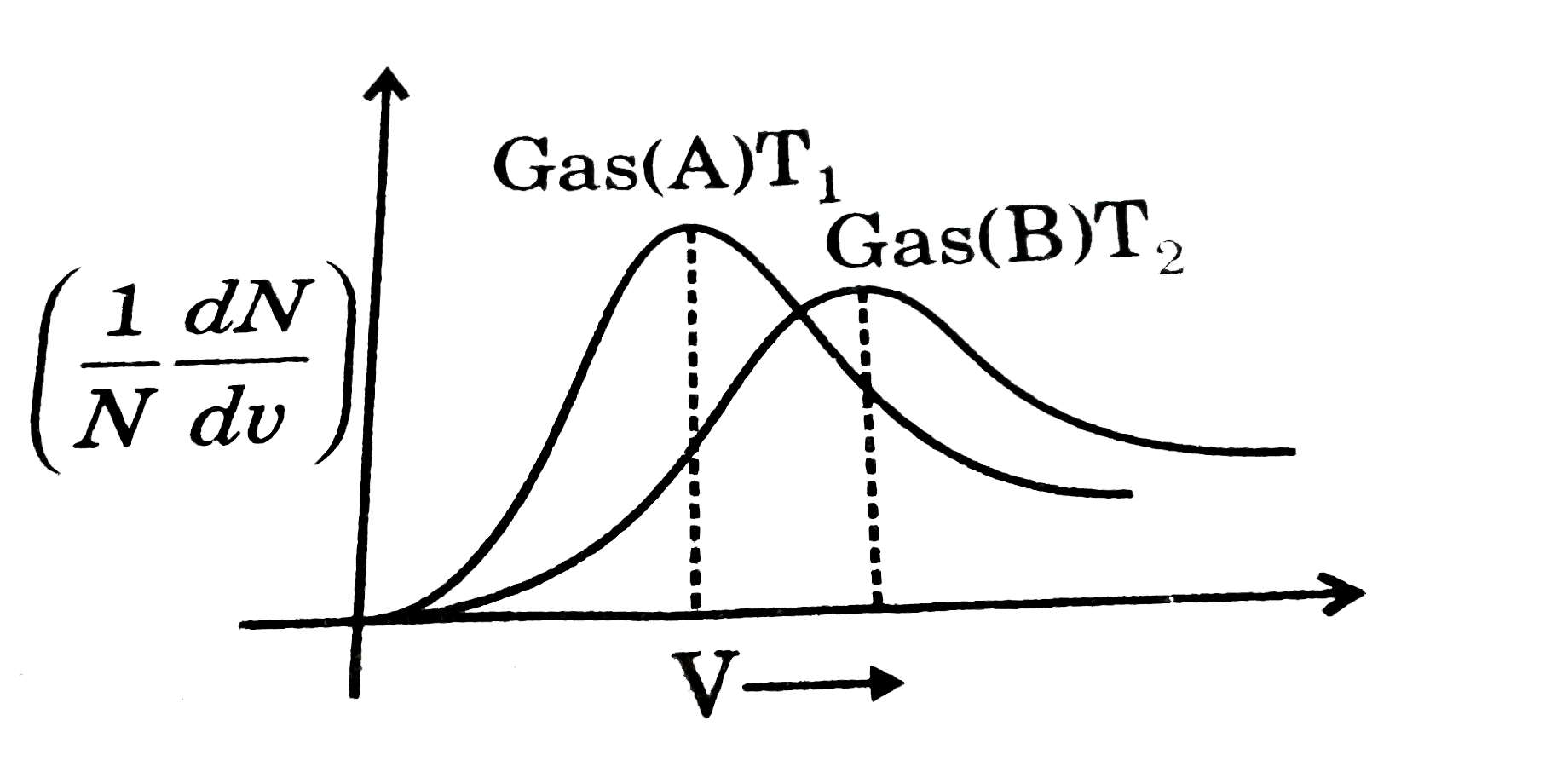
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
If two gases A and B and at temperature TAandTB respectivley have identical Maxwellian plots then which of the following statement are true?
View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
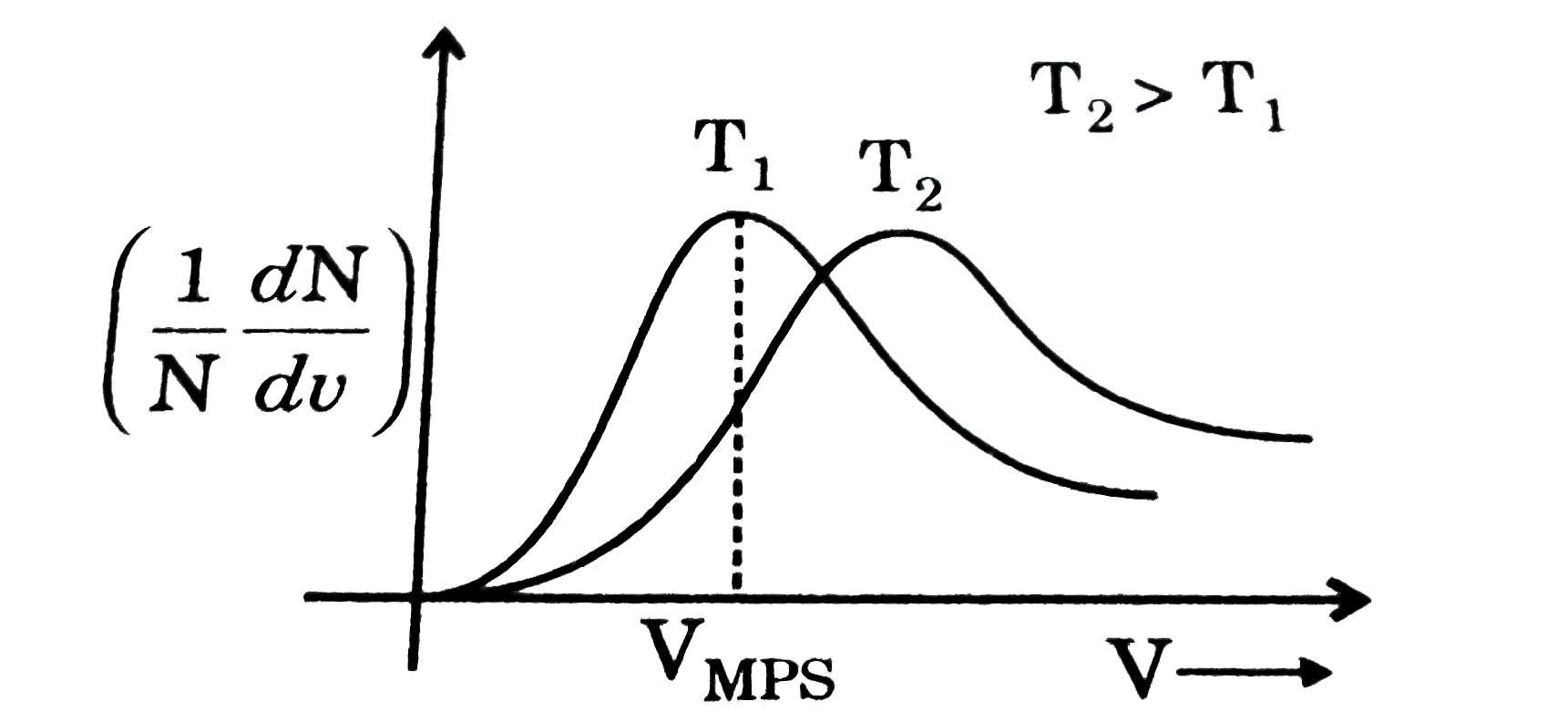
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
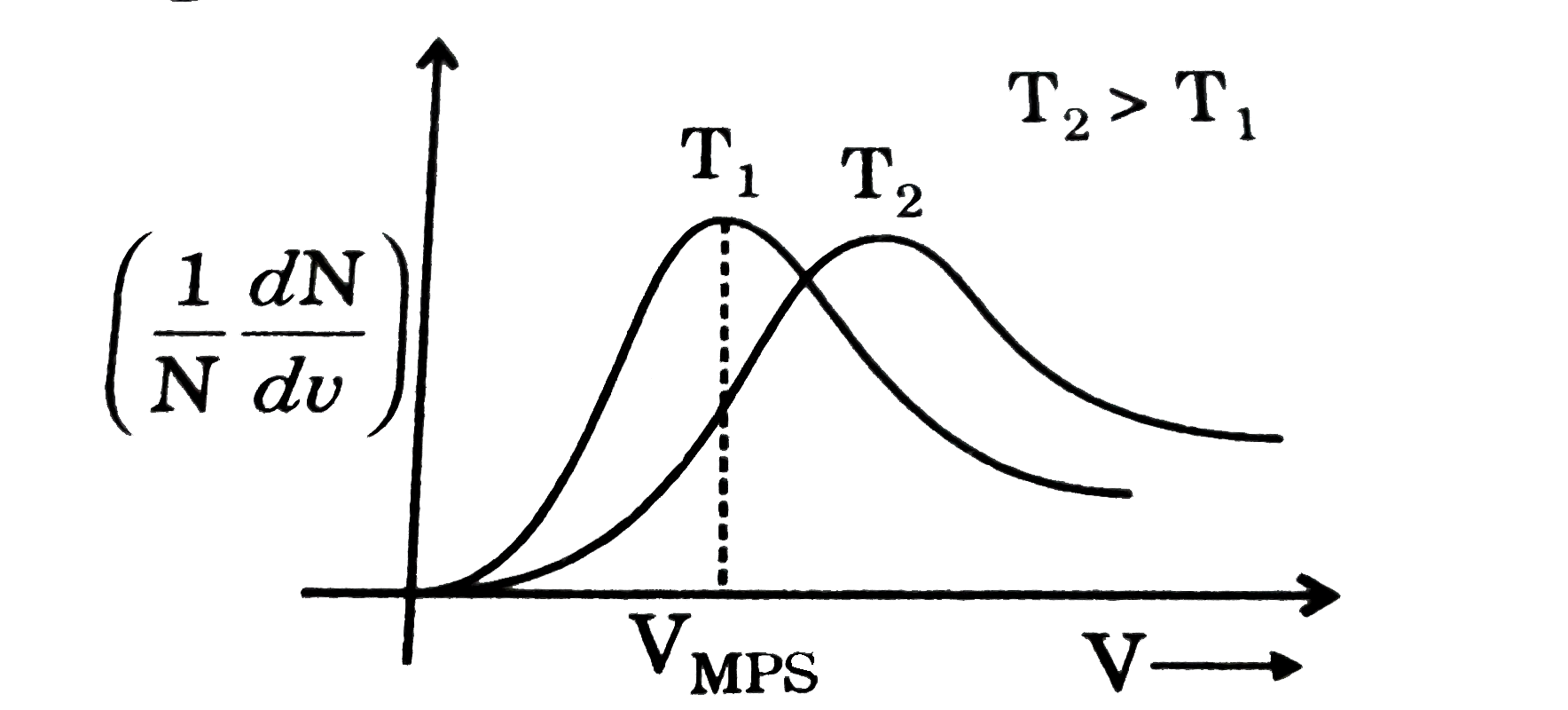
If a gas sample contains a total of N molecules. The area under any given maxwellian plot is equal ot :
View Solution