Question

Given in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Explanation

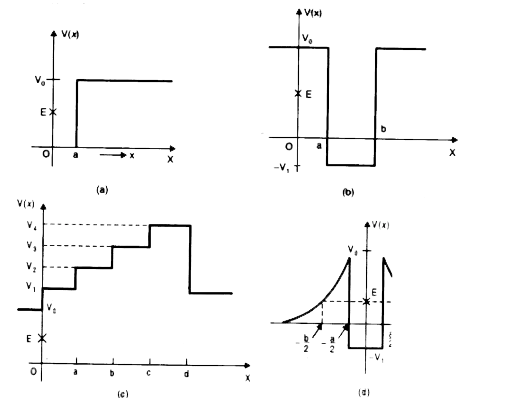
We know, that total energy `E=K.E+P.E` or `K.E=E-P.E` and kinetic energy can never be negative. The object can not exists in the region, where its K.E. Would become negative. A) IN the region between x=0 and x=a, potential energy is zero. So, kinetic energy will be negative in this region. Thus, the particle cannot be present in the region xgta. The minimum total energy that the particle can have in this case is zero.