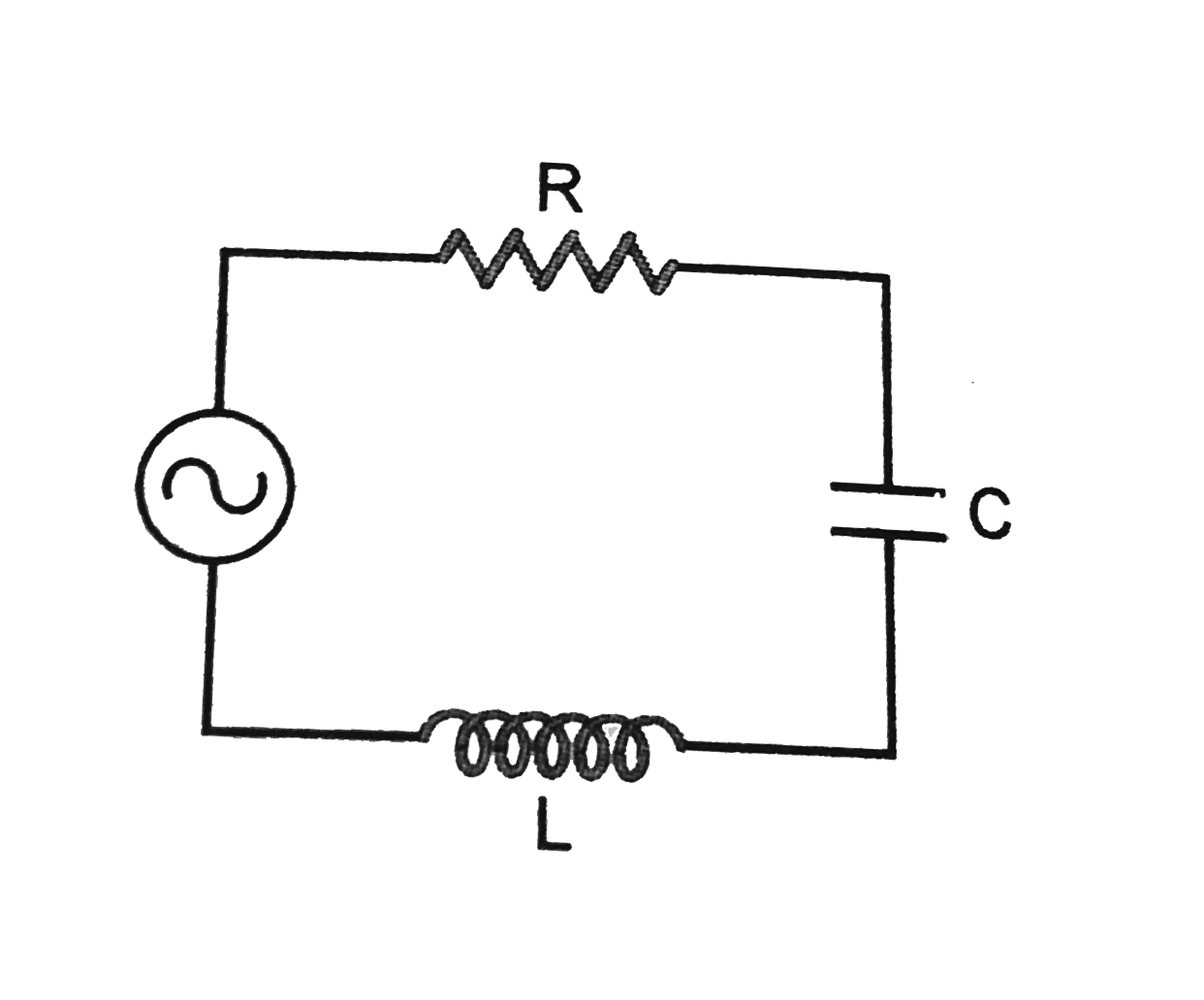
A series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops across the three elements the circuits. Show that the potential drop across the LC combination is zero at the resonating frequency.
Inductance of the inductor,L=5.0H
Capacitance of the capacitor, C=80μH=80×10−6F
Resistance of the resistor, R=40Ω
Potential of the variable voltage source, V=230V
(a) Resonance angular frequency is given as:
ωR=1√LC
=1√5×80×10−6=10320=50rad/s
Hence, the circuit will come in resonance for a source frequency of 50 rad/s.
(b) Impedanc of the circuit is given by the relation,
Z=√R2+(ωL−1ωC)2
At resonance,
ωL=1ωC
∴Z=R40Ω
Amplitude of the current at the resonating frequency is given as I0=V0Z
where,
v0= Peak voltage
=√2V
∴I0=√2VZ
=√2×23040=8.13A
Hence, at resonance, the impedance of the circuit is 40 Ω and the amplitude of the current is 8.13A.
(c) RMS potential drop cross the inductor,
(VL)rms=I×ωRL
Whre,
I=rms current
=I0√2=√2V√2Z=23040A
∴(VL)rms=23040×50×5=1437.5V
Potential drop across the capacitor,
Vc)Rms=l×LωRC
=23040×150×80×10−6=1437.5V
Potential drop across the resistor.
(VR)rms=IR
23040×40=230V
Potential drop across the LC combination,
VLC=I(ωRL−1ωRC) ltbgt At resonance, (ωRL−1ωRC)
∴VLC=0
Hence, it is proved that the potential drop across the LC combination is zero zt resonating frequency.
Topper's Solved these Questions
Similar Questions
A series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops acorss the three elements the circuits. Show that the potential drop acorss the LC combination is zero at the resonating frequecny.

View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.
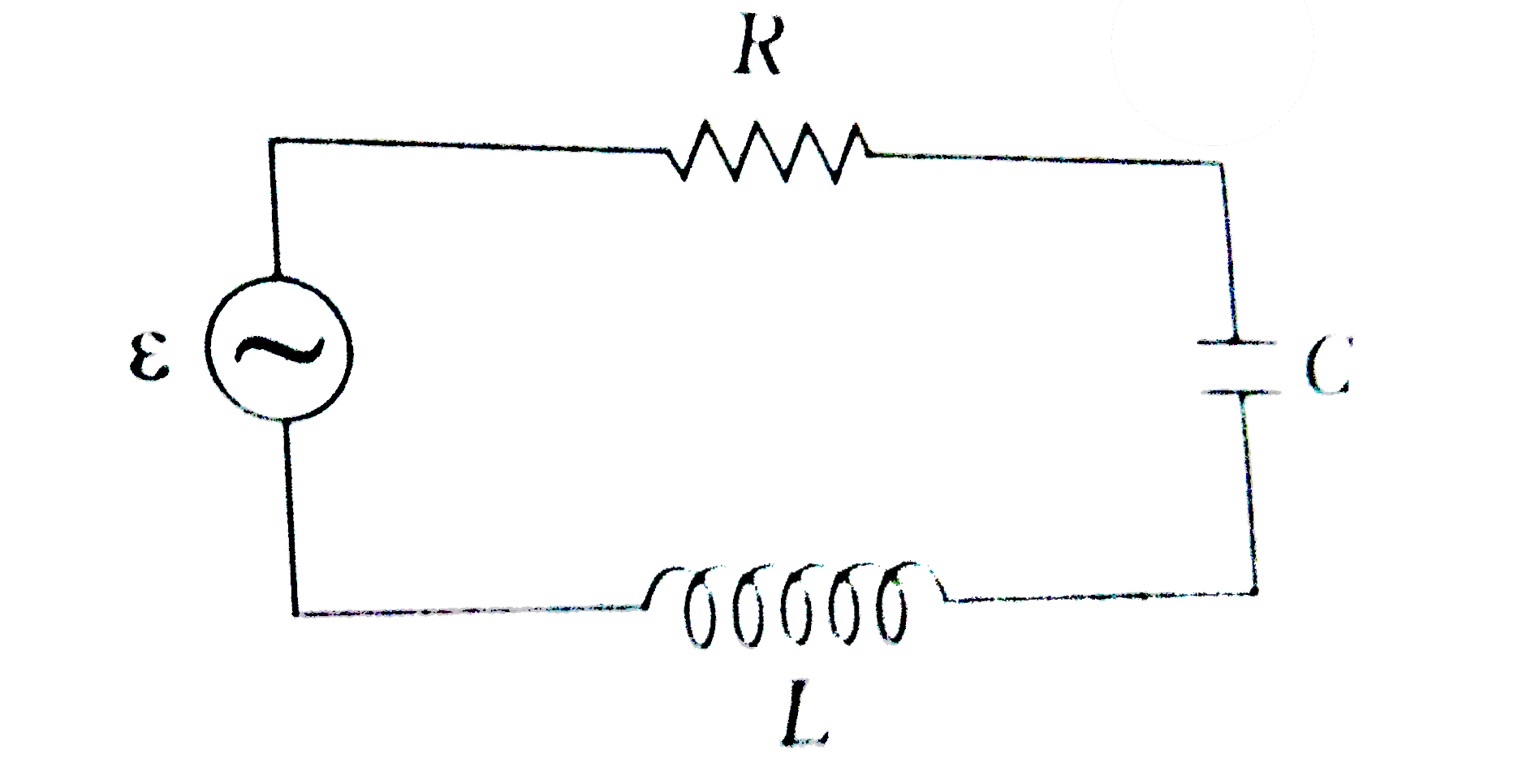
View Solution
Knowledge Check
For the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency
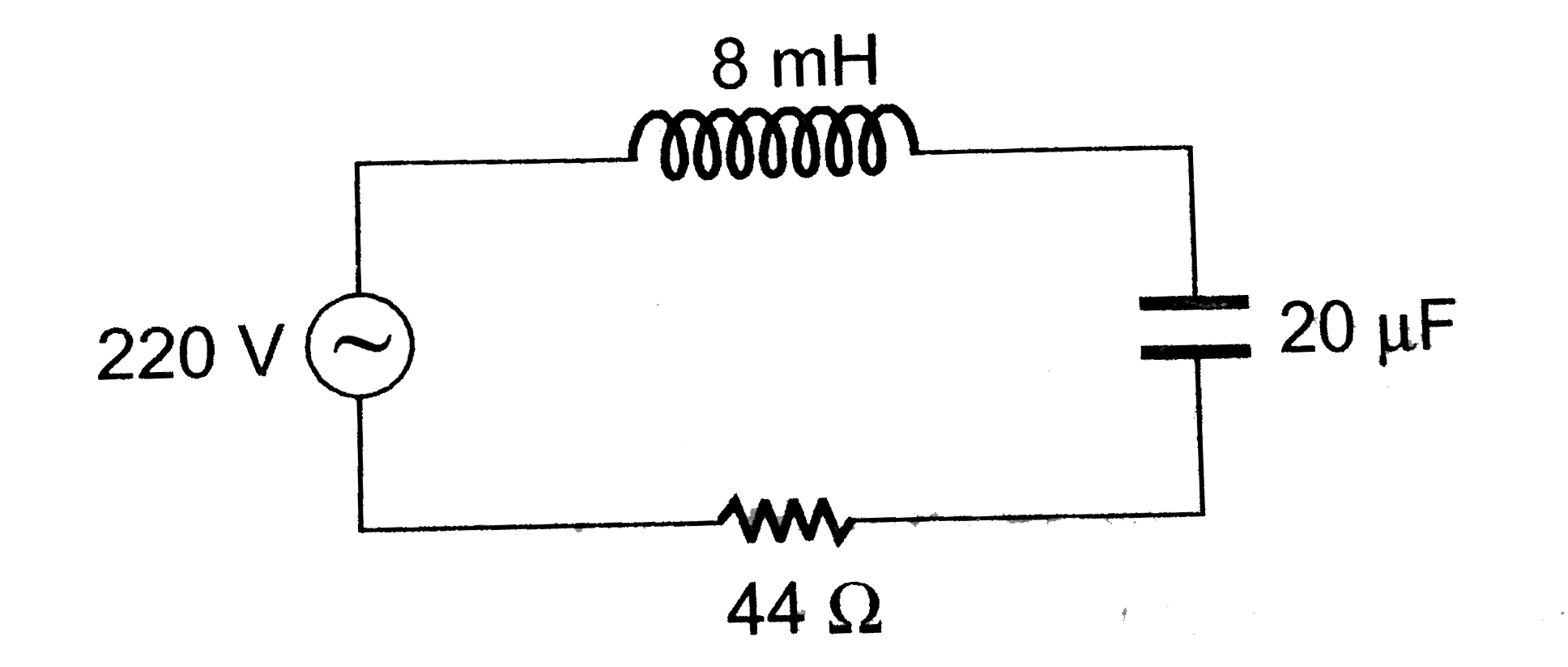 A2500rads−1 and 5√2AB2500rads−1 and 5AC2500rads−1 and 5√2AD25rads−1 and 5√2A
A2500rads−1 and 5√2AB2500rads−1 and 5AC2500rads−1 and 5√2AD25rads−1 and 5√2AAt resonance frequency the impedance in series LCR circuit is
AmaximumBminimumCzeroDinfinityIn a series LCR circuit, at resonant frequency.
Athe impedance and the current are maximumBthe impedance is maximumCthe current and voltage are maximumDthe current and voltage are minimum
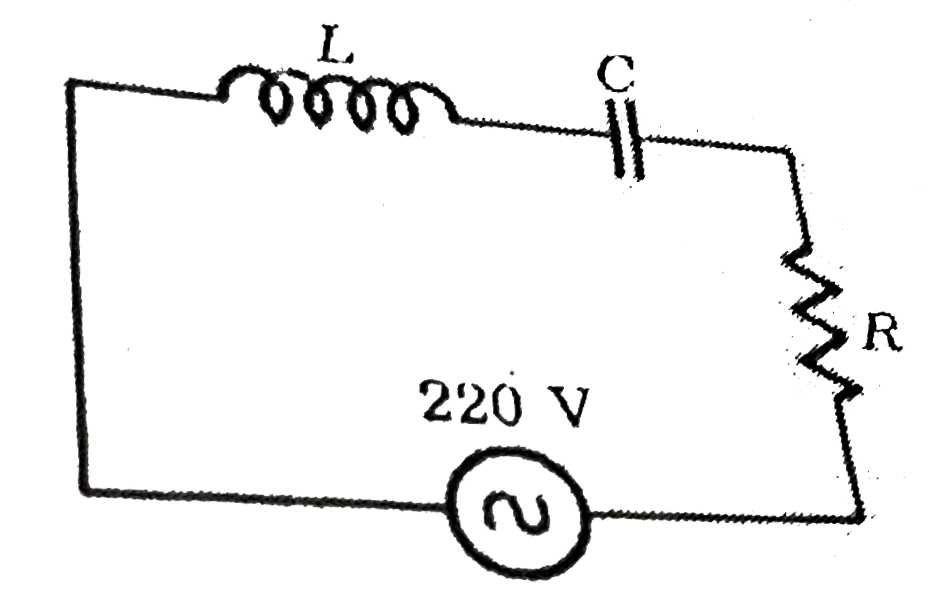
Fig 14.18 shows a series LCR circuit connected to a variable frequency 200 V source:
L=4.0H,C=100μF and R=40Ω.
(i) Calculate the resonant frequency of the circuit.
(ii) Obtain the impedance of the circuit and the amplitude of the current at resonating frequency.
(iii) Determine r.m.s. potential drop across L.
View SolutionA variable frequency 230 V alternating voltage source is connected across a series combination of L=5.0H,C=80μF and R=40Ω
(i) Calculate the angular frequency fo the source which drives the circuit in resonance.
(ii) Obtain r.m.s. the impedance of the circuit and amplitude of current at resonance frequency
(iii) Obtain r.m.s. potential drop across the three elements of the circuit at resonating frequency.
(iv) How do you explain the observation that the algerbraic sum of voltages across the three elements obtained is greater than the supplied voltage.
View SolutionA series LCR circuit with L=80mH,C=50μF and R=60ohm is connected to a variable frequency 220 V source. Determine (i) the source frequency which drives the circuitin resonance (iii) the quality factor Q of the circuit.
View SolutionA series LCR circuit is shown in the figure below.

Determine the source frequency which drives the circuit in resonance . Also obtain the value of Q - factor of the circuit.
View SolutionA series LCR circuit with L=4.0h,C=100μF and R=60Ω is connected to a varialbe frequency 240 V source. Calcalate
(i) angular frequency of the source which drives the circuit in resonace,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductro at resonance.
View Solution
