While calculating eh mean and variance of 10 readings, a student wrongly used the reading of 52 for the correct reading 25. He obtained the mean and variance as 45 and 16 respectively. Find the correct mean and the variance.
Video Solution
Text Solution
Number of observations n=10
Mean,
¯x=45
Variance σ2=16
Now, incorrect mean,
¯x=45
⇒incorrect ∑xi10=45
⇒ incorrect ∑xi=450
Then, correct∑xi=450−52+25=423
⇒ correct mean= correct ∑xi10=42310=42.3
Incorrect variance,
(σ)2=16
⇒ 16=incorrect ∑(xi)210−452
⇒ incorrect ∑(xi)2=10(16+2025)=20410
Correct,
∑x2i=20410−(52)2+(25)2=18331
Now,
correct variance= 1833110−(42.3)2=1833.1−1789.29=43.81
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The mean and variance of a binomial distribution are 6 and 4 respectively, then n is
A9B12C18D10
Find the mean and variance for each of the data :
 View Solution
View Solutionfind the binomial distribution for which the mean and variance are 12 and 3 respectively .
View SolutionCalculate the mean and variance from the data given below:
 View Solution
View SolutionFind the mean and variance of first 10 multiples of 3.
View SolutionIn calculating the mean of 35 observations, a student wrongly copies a reading as 135 and gets the mean 0.3 more than the true mean.
View SolutionFind the mean and variance for each of the data in Question:
 View Solution
View SolutionFind the mean and variance for each of the data in Question:
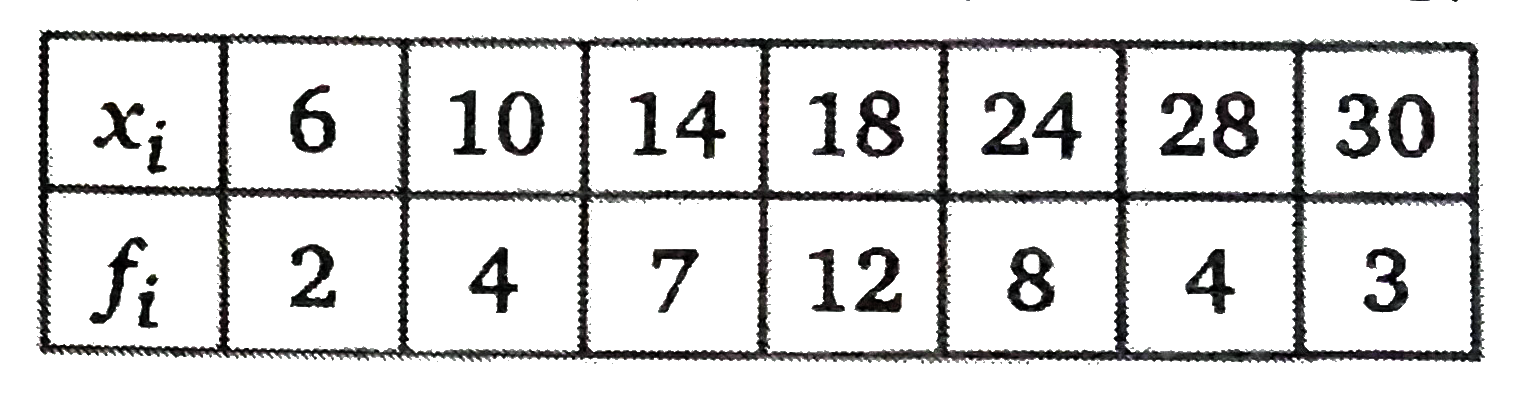 View Solution
View Solution