A bullet of mass 10 g moving horizontally with a velocity of strikes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5 m. As a result, the centre of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
The correct Answer is:C
To solve the problem, we will use the principles of conservation of momentum and energy.
Step 1: Understand the scenario
A bullet of mass mb=10g=0.01kg is moving with a velocity vb=400m/s and strikes a wooden block of mass mB=2kg. After the bullet passes through the block, the block rises a vertical distance of h=10cm=0.1m.
Step 2: Calculate the potential energy gained by the block
When the block rises to a height h, it gains potential energy given by:
PE=mB⋅g⋅h
where g=9.81m/s2 (acceleration due to gravity).
Substituting the values:
PE=2kg⋅9.81m/s2⋅0.1m=1.962J
Step 3: Relate the potential energy to the kinetic energy of the block
The potential energy gained by the block is equal to the kinetic energy it had just after the bullet passed through it. The kinetic energy (KE) of the block can be expressed as:
KE=12mBv2B
where vB is the velocity of the block just after the bullet passes through it.
Setting the potential energy equal to the kinetic energy:
1.962J=12(2kg)v2B
Step 4: Solve for the velocity of the block
Rearranging the equation:
v2B=1.962J⋅22kg=1.962m2/s2
vB=√1.962≈1.4m/s
Step 5: Apply conservation of momentum
Before the collision, the momentum of the system is given by the bullet alone:
pinitial=mbvb=0.01kg⋅400m/s=4kg m/s
After the bullet passes through the block, the momentum is the sum of the momenta of the bullet and the block:
pfinal=mbvb′+mBvB
where vb′ is the velocity of the bullet after it exits the block.
Setting the initial momentum equal to the final momentum:
4=0.01vb′+2⋅1.4
4=0.01vb′+2.8
Step 6: Solve for the final velocity of the bullet
Rearranging gives:
0.01vb′=4−2.8=1.2
vb′=1.20.01=120m/s
Conclusion
The speed of the bullet after it emerges horizontally from the block is approximately 120m/s.
---
A bullet of mass mb=10g=0.01kg is moving with a velocity vb=400m/s and strikes a wooden block of mass mB=2kg. After the bullet passes through the block, the block rises a vertical distance of h=10cm=0.1m.
When the block rises to a height h, it gains potential energy given by:
PE=mB⋅g⋅h
where g=9.81m/s2 (acceleration due to gravity).
PE=2kg⋅9.81m/s2⋅0.1m=1.962J
The potential energy gained by the block is equal to the kinetic energy it had just after the bullet passed through it. The kinetic energy (KE) of the block can be expressed as:
KE=12mBv2B
where vB is the velocity of the block just after the bullet passes through it.
1.962J=12(2kg)v2B
Rearranging the equation:
v2B=1.962J⋅22kg=1.962m2/s2
vB=√1.962≈1.4m/s
Before the collision, the momentum of the system is given by the bullet alone:
pinitial=mbvb=0.01kg⋅400m/s=4kg m/s
pfinal=mbvb′+mBvB
where vb′ is the velocity of the bullet after it exits the block.
4=0.01vb′+2⋅1.4
4=0.01vb′+2.8
Rearranging gives:
0.01vb′=4−2.8=1.2
vb′=1.20.01=120m/s
The speed of the bullet after it emerges horizontally from the block is approximately 120m/s.
Topper's Solved these Questions
Similar Questions
A bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
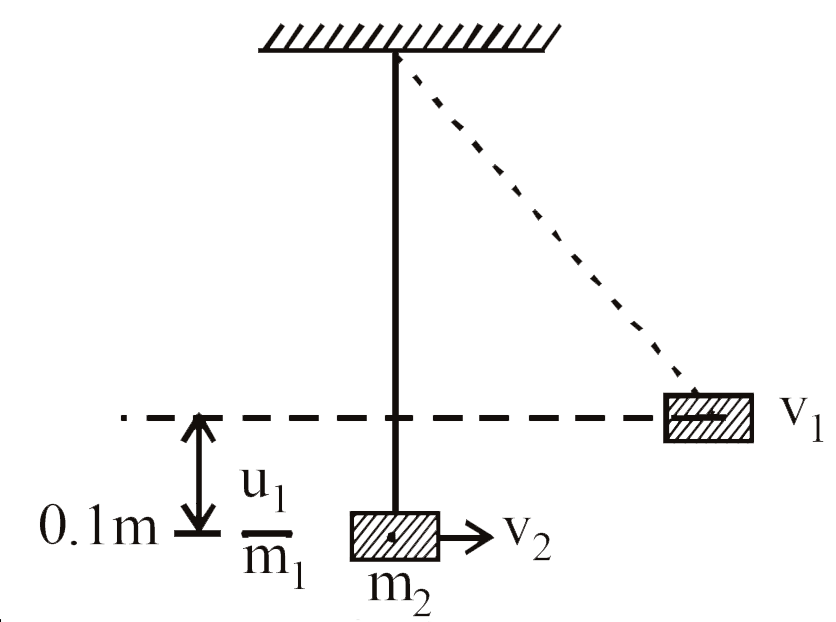
View SolutionA bullet of mass 0.01J kg and travelling at a speed of 500m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The cnetre of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
View Solution
Knowledge Check
A bullet of mass 10g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light in-extensible string of length 5m. As a result, the center of gravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out horizontally from the block will be
A120ms−1B160ms−1C100ms−1D80ms−1A bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wook block of mass 2 kg which is suspended by light inextensible string of length 5 m. As a result, the centre of gravity of the block found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
A100ms−1B80ms−1C120ms−1D160ms−1A bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
A15ms−1B20ms−1C100ms−1D50ms−1
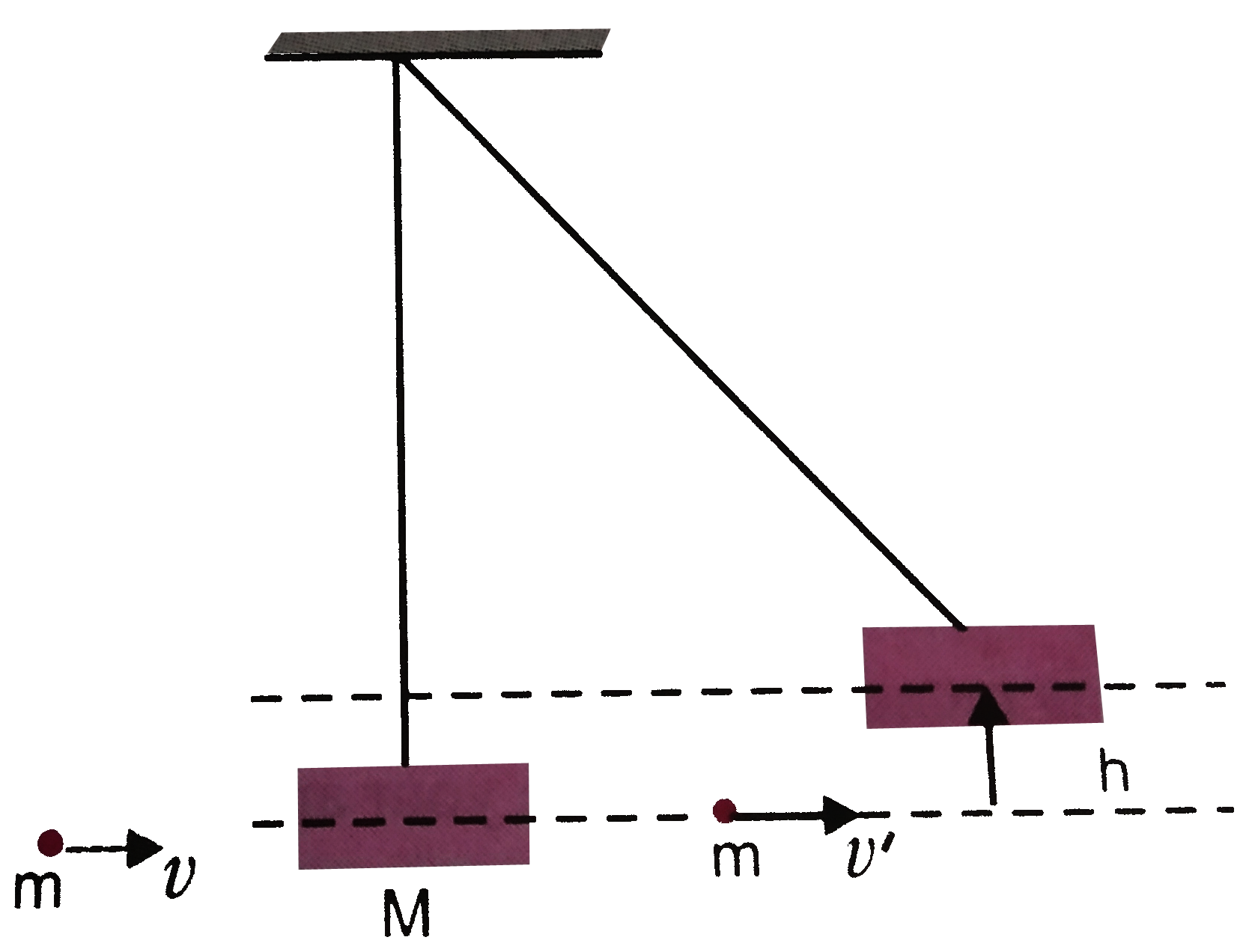
A bullet of mass 20 g moving horizontally at speed of 300 m/s is fired into wooden block of mas 500 suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass 20 kg travelling horizontally at 100ms−1 gets embedded at the centre of a block of wood of mass 1kg, suspended by a light vertical string of 1m in length. Calculate the maximum inclination of the string to the vertical.
View SolutionA bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5 m. As a result, the centre of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionA bullet of mass 10 g moving with a velocity of 400 m/s gets embedded in a freely suspended wooden block of mass 900 g. What is the velocity acquired by the block ?

View Solution
