Let a,b, and c be three real numbers satistying $[a, b, c] ⎡ ⎢ ⎣ \begin{matrix} 1 & 9 & 7 8 & 2 & 7 7 & 3 & 7 \end{matrix} ⎤ ⎥ ⎦ = [0, 0, 0]$ Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation $a x^{2} + b x + c = 0 t h e n \infty \sum n = 0 {(\frac{1}{α} + \frac{1}{β})}^{n}$ is (A) 6 (B) 7 (C) $\frac{6}{7}$ (D) oo

$6 / 7$

$\infty$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Let a,b, and c be three real numbers satistying [a,b,c][(1,9,7),(8,2,7),(7,3,7)]=[0,0,0]Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation ax^2+bx+c=0 then sum_(n=0)^oo (1/alpha+1/beta)^n is (A) 6 (B) 7 (C) 6/7 (D) oo by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBER

Topper's Solved these Questions

Knowledge Check

Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n$ is
A6
B7
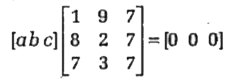C $\frac{6}{7}$
D $\infty$
If $α$ and $β$ are the roots of the , quadratic equation , $a x^{2} + b x + c = 0$ ,with $α < β$ ,then for $x < α$ (or) $x > β$ , $a x^{2} + b x + c$ and $a$ have ,
(A) Opposite sign
(B) Positive sign
(C) same sign
(D) none of these
Arational numbers
Breal and negative
Cnegative real parts
Dnone of these
If $α$ and $β$ are the roots of the equation $a x^{2} + b x + c = 0$ , then $\frac{α}{α β + b} + \frac{β}{a α + b}$ is equal to
A $\frac{2}{a}$
B $\frac{2}{b}$
C $\frac{2}{c}$
D $- \frac{2}{a}$

MOTION-COMPLEX NUMBER -EXERCISE - 4 (LEVEL -II) PREVIOUS YEAR - JEE ADVANCED

Home
Ask Doubt
Profile

Let a,b, and c be three real numbers satistying [a,b,c]⎡⎢⎣197827737⎤⎥⎦=[0,0,0]Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation ax2+bx+c=0then∞∑n=0(1α+1β)n is (A) 6 (B) 7 (C) 67 (D) oo

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let b=6 with a and c satisfying (1). If α and β are the roots of the quadeatic equation ax2+bx+c=0,then is

If α and β are the roots of the , quadratic equation ,ax2+bx+c=0 ,with α<β ,then for x<α (or) x>β, ax2+bx+c and a have , (A) Opposite sign (B) Positive sign (C) same sign (D) none of these

If α and β are the roots of the equation ax2+bx+c=0, then ααβ+b+βaα+b is equal to

MOTION-COMPLEX NUMBER -EXERCISE - 4 (LEVEL -II) PREVIOUS YEAR - JEE ADVANCED

Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n$ is

If $α$ and $β$ are the roots of the , quadratic equation , $a x^{2} + b x + c = 0$ ,with $α < β$ ,then for $x < α$ (or) $x > β$ , $a x^{2} + b x + c$ and $a$ have ,
(A) Opposite sign
(B) Positive sign
(C) same sign
(D) none of these

If $α$ and $β$ are the roots of the equation $a x^{2} + b x + c = 0$ , then $\frac{α}{α β + b} + \frac{β}{a α + b}$ is equal to