There are 12 guests at a dinner party. Supposing that the master and mistress of the house have fixed seats opposite one another, and that there are two specified guests who must always, be placed next to one another, the number of ways in which the company can be placed is
20.10 !
22.10 !
44.10 !
none
The correct Answer is:A
Step by step video, text & image solution for There are 12 guests at a dinner party. Supposing that the master and mistress of the house have fixed seats opposite one another, and that there are two specified guests who must always, be placed next to one another, the number of ways in which the company can be placed is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - THEORY AND EXERCISE BOOKEXERCISE - EXERCISE - 2 (LEVEL -II)18videos
THEORY AND EXERCISE BOOK
- BOOK - MOTIONCHAPTER - THEORY AND EXERCISE BOOKEXERCISE - EXERCISE -323videos
THEORY AND EXERCISE BOOK
- BOOK - MOTIONCHAPTER - THEORY AND EXERCISE BOOKEXERCISE - EXERCISE - 4 (LEVEL -II)22videos
THEORY AND EXERCISE BOOK
- BOOK - MOTIONCHAPTER - TANGENT & NORMALEXERCISE - EXERCISE 414videos
TANGENT & NORMAL
- BOOK - MOTIONCHAPTER - THREE DIMENSIONAL GEOMETRY (3 -D)EXERCISE - SOLVED EXAMPLE33videos
THREE DIMENSIONAL GEOMETRY (3 -D)
Similar Questions
There are 2n guests at a dinner party. Supposing that the master and mistress of the house have fixed seats opposite one another and that there are two specified guests who must not be placed next to one another, show that the number of ways in which the company can be placed is (2n−2)!×(4n2−6n+4).
View Solution12 guests at a dinner party are to be seated along a circular table. Supposing that the master and mistress of the house have fixed seats opposite to one another and that there are two specified guests who must always be placed next to one another. The number of ways in which the company can be placed, is
View Solution
Knowledge Check
- Question 1 - Select One
Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
 A25B26C27D30
A25B26C27D30 - Question 2 - Select One
Eighteen guests have to be seated half on each side of a long table. Four particular guests desire to sit on one particular side and three others on other side. Determine the number of ways in which the sitting, arrangements can be made.
A18!B462×(9!)2C(9!)2D7×(9!)2 - Question 3 - Select One
A man invites a party to (m+n) friends to dinner and places m at one round table and n at another. The number of ways of arranging the guests is
A(m+n)!m!n!B(m+n)!(m−1)!(n−1)!C(m−1)!(n−1)!Dnone of these
Three person A,B,C invite 2n guest to a party. All the people sit around a round table such A,B,C have their fixed seats (there is a least one seat between any two fixed seats)a and two particulars guests doesn't sit together. Find the number of ways is whcih they can be seated.
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
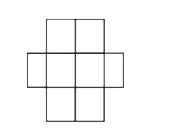 View Solution
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
 View Solution
View SolutionEight guests have to be seated 4 on each side of a long rectangular table.2 particular guests desire to sit on one side of the table and 3 on the other side. The number of ways in which the sitting arrangements can be made is
View SolutionA man invites 10 friends to a party and places 5 at one table and 5 at another table, the tables being round. The number of ways in which he can arrange his friends is :
View Solution

