Let ABC be a triangle such that the coordinates of A are (–3, 1). Equation of the median through B is 2x + y – 3 = 0 and equation of the angular bisector of C is 7x – 4y – 1 = 0. Then match the entries of column-I with their corresponding correct entries of column-II

The correct Answer is:(A)–R ; (B)–S ; (C)–Q
Step by step video & image solution for Let ABC be a triangle such that the coordinates of A are (–3, 1). Equation of the median through B is 2x + y – 3 = 0 and equation of the angular bisector of C is 7x – 4y – 1 = 0. Then match the entries of column-I with their corresponding correct entries of column-II by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 4 Lelvel -I
15 Videos
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 4 Lelvel -II
7 Videos
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 3
27 Videos
- SOLUTION OF TRIANGLEBOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 4( LEVEL II)
10 Videos
- TANGENT & NORMALBOOK - MOTIONCHAPTER - TANGENT & NORMALEXERCISE - EXERCISE 4
14 Videos
Similar Questions
Let ABC be a triangle such that the coordinates of the vertex A are (3, 1). Equation of the median through B is 2x+y−3=0 and equation of the angular bisector of C is 7x−4y−1=0. Find the slope of line BC.
View SolutionIf α and β are the roots of the equation, acosθ+bsinθ=c, then match the entries of column I with the entries of column- II

View Solution
Knowledge Check
In a triangle ABC, coordinate of A are (1,2) and the equations of the medians through B and C are respectively, x+y=5&x=4. Then area of ΔABC (in sq. units) is:
A12B9C4D5In a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of median through A isAx+y=4B5x−3y=1C5x+3y=1D5x=3yIn △ABC, the coordinates of the vertex A are , (4,−1) and lines x−y−1=0and2x−y=3 are the internal bisectors of angles B and C . Then the radius of the circles of triangle AbC is
A5√5B3√5C6√5D7√5
Match the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.
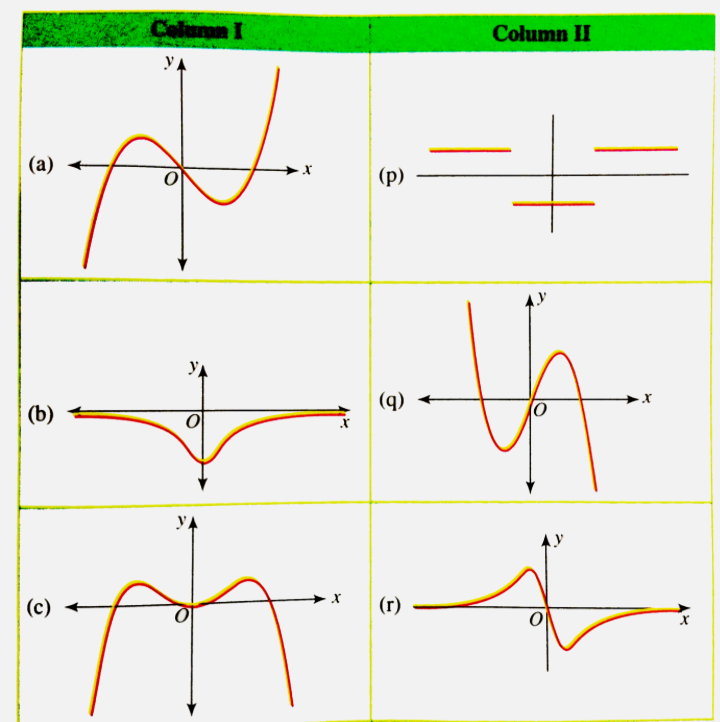
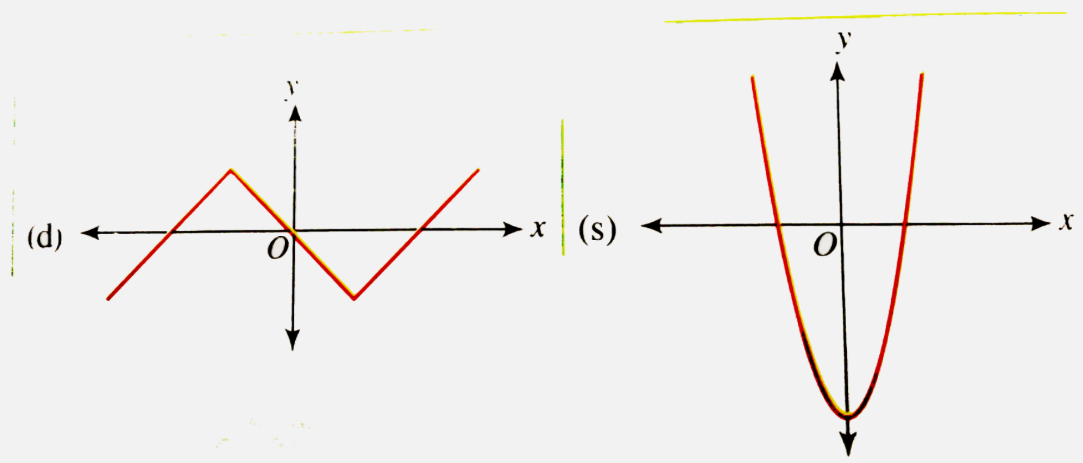
View Solutionin a triangle ABC, if A is (1,2) and the equations of the medians through B and c are x+y=5 and x=4 respectively then B must be:
View SolutionLet in ΔABC coordinates of vertex A is (0,0). Equation of the internal angle bisector of ∠ABC is x+y−1=0 and mid-point of BC is (1,3). The ordinate of vertex C is
View SolutionEquation of angle bisector of the lines 3x-4y+1=0 and 12x+5y-3=0 containing the point (1,2)
View SolutionA(1,3)andc(−25,−25)are the vertices of a ΔABCandthe equation of the angle bisector of ∠ABC is x+y=2.
View Solution
