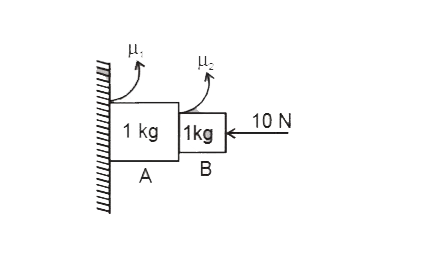
Find the accelerations of blocks A and B for the following cases.
(A) μ1=0 and μ2=0.1 (P)aA=aB=9.5m/s2
(B) μ2=0 and μ1=0.1 (Q)aA=9m/s2,aB=10m/s2
(C) μ1=0.1 and μ2=1.0 (R)aA=aB=g=10m/s2
(D) μ1=1.0 and μ2=0.1 (S)aA=1,aB=9m/s2
(a) R, (b) Q, (c) P, (d) S
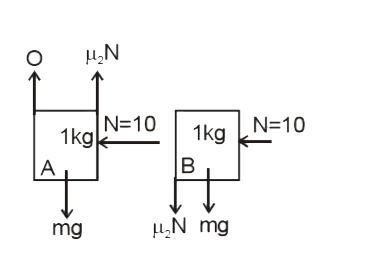
(i) FBD in (case(i))
{μ1=0,μ2=0.1}
While friction’s work is to oppose the relative motion and here if relative motion will start then friction comes and without relative motion there is no friction so both the block move together with same acceleration and friction will not come.
 ⇒=aA=aB=10m/s2
⇒=aA=aB=10m/s2
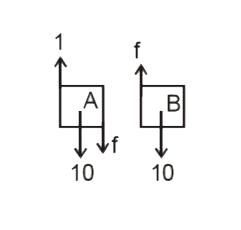
(ii) Friction between wall and block A oppose relative motion since wall is stationary so friction wants to slop block A also and maximum friction will act between wall and block while there is no friction between block.
Note : Friction between wall and block will oppose relative motion between wall and block only it will not do anything for two block motion.
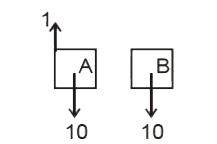
aA=9m/s2,aB=10m/s2
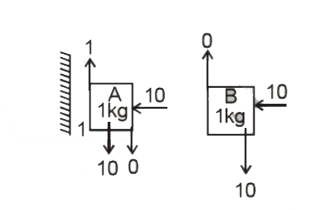
(iii) 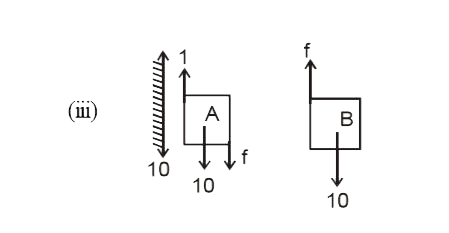
Friction between wall and block will be applied maximum equal to 1N but maximum friction available between block A and B is 10 N but if this will be there then relative motion will increase while friction is to oppose relative motion. So friction will come less than 10 so friction will be f that will be static.
for system (20 - 1) =2×a
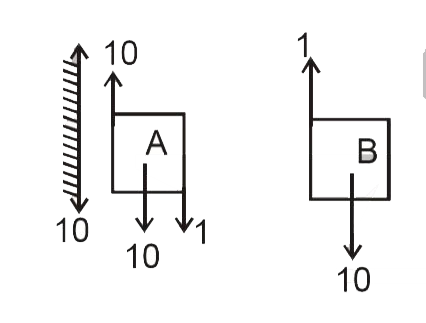
rArr a=19/2=9.5m//s^(2)<br>(iv)a_(A)=(11-10)/1=1m//s^(2)<br>a_(B)=(10-1)/1=9m//s^(2)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXAMPLE47videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - SOLVED EXAMPLE16videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B12videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN12videos
ONE DIMENSION MOTION
Similar Questions
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then the value of c is
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0, then the value of 'c' is:
View Solution
Knowledge Check
- Question 1 - Select One
If the equation of the locus of a point equidistant from the points (a1,b1, and (a2,b2) is
(a1−a2)x+(b1−b2)y+c=0, then the value of c isA12(a22+b22)−(a21−b21)B(a21−a22+b21−b22)C12(a21+a22+b21+b22)D√(a21+b21−a22−b22) - Question 2 - Select One
The equation of a plane containning the lines r=a1+t b1andr=a2+t b2, where [(a2−a1)b1b2]=0 is
A[(r+a1)⋅(b1×b2)]=1B[(r−b1)⋅a⋅(b1×b2)]=0C[(r−a1)⋅(b1×b2)]=0DNone of these - Question 3 - Select One
In which of the following cases the friction force between 'A' and 'B' is maximum. In all cases μ1=0.5,μ2=0.
A B
B C
C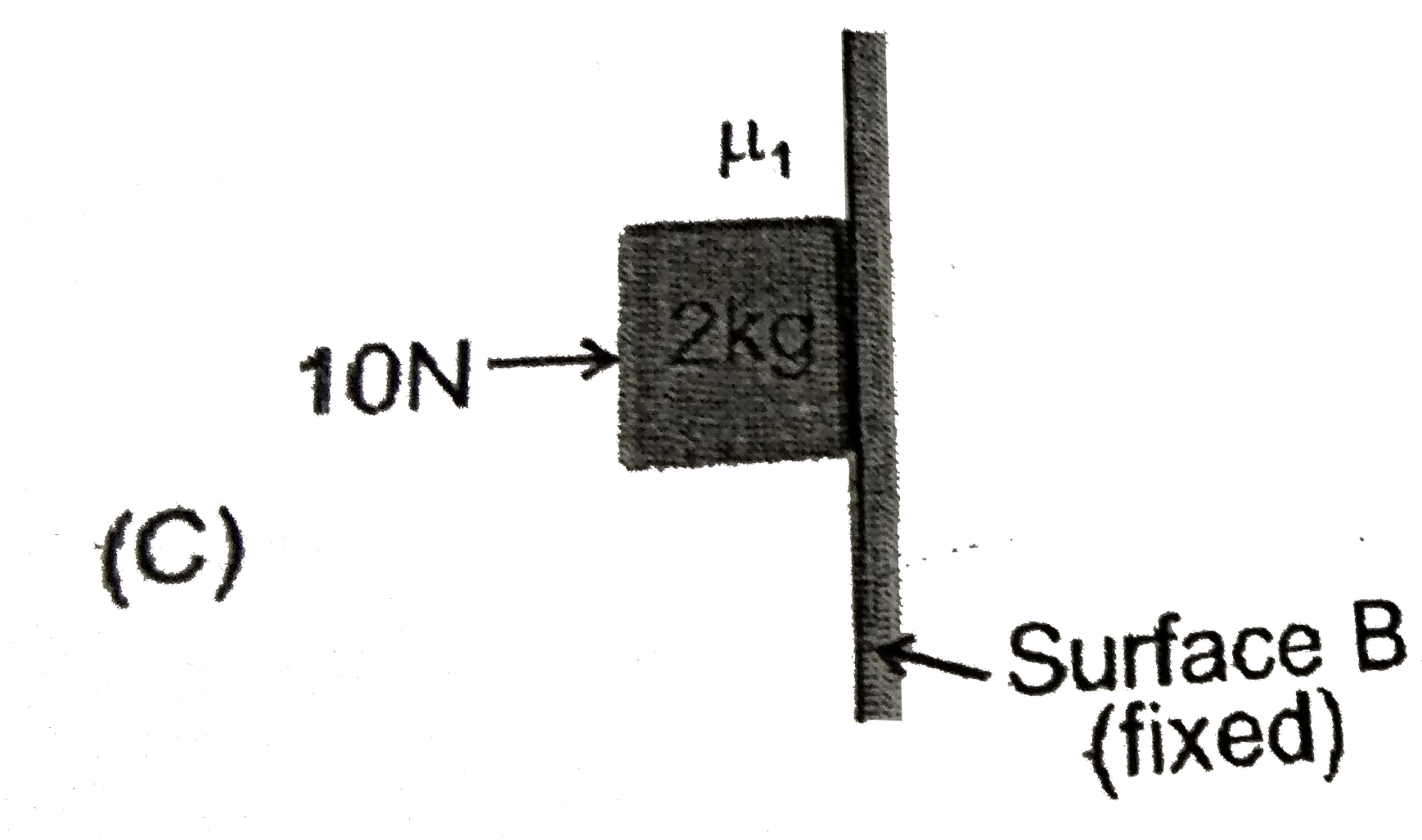 D
D
In the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
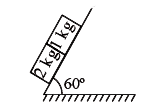 View Solution
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a−1−a2)x+(b1−b2)y+c=0 , then the value of c is
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
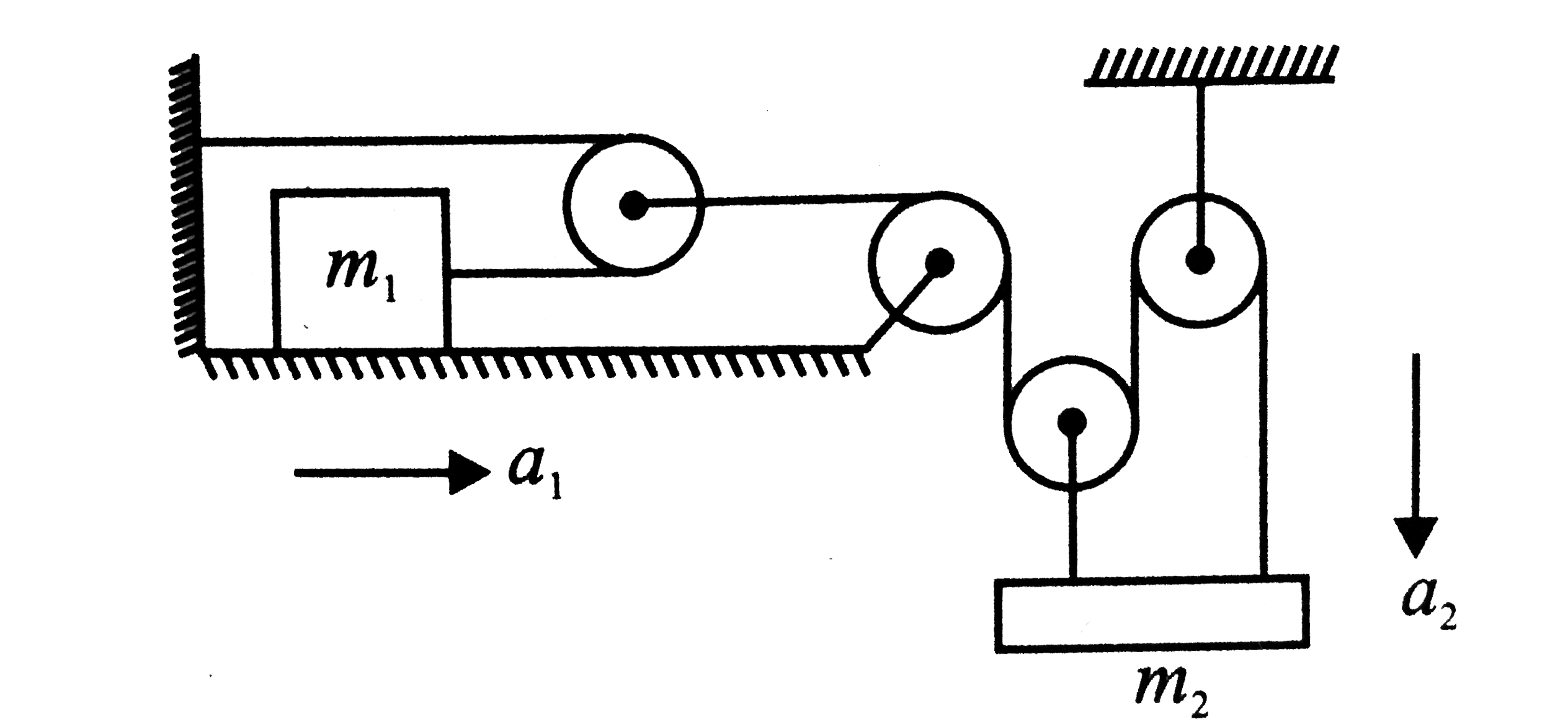 View Solution
View SolutionIf A1 and A2 are two A.M.'s between a and b, prove that
(i) (2A1−A2)(2A2−A1)=ab
(ii) A1+A2=a+bView SolutionIf the ratio of the roots of a1x2+b1x+c1=0 be equal to the ratio of the roots of a2x2+b2+c2=0, then a1a2,b1b2,c1c2 are in
View Solution

