A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
zero
hdg
h2dg
2 hdg
The correct Answer is:C
Step by step video, text & image solution for A beaker is filled with a liquid of density rho upto a height h If the beaker is at rest, the mean pressure at the walls is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-2 (ASSERTION AND REASON)
28 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-3 SECTION-A (PREVIOUS YEAR PROBLEM)
61 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - QUESTIONS FOR PRACTICE
6 Videos
- HEAT-2 BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)
30 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
6 Videos
Similar Questions
Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View SolutionA wooden ball of density σ is released from the bottom of a tank which is filled with a liquid of density ρ(ρ>σ)up to a height h1. The ball rises in the liquid, emerges from its surface and attains a height h2 in air.If viscous effects are neglected,the ratio h2h1 is
View Solution
Knowledge Check
A cylinder is fill ed with a liquid of density p upto a height h. What is the hydrostatic pressure exerted by the liquid on the bottom of the cylinder, if the cylinder is kept in a lifi moving upwa rds with an acceleration a ?
AρghBρ(g+a)Cρ(g−a)DρghaAn observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A52B√52C√32D32
A52B√52C√32D32An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A5/2B√(5/2)C√(3/2)D3/2
A5/2B√(5/2)C√(3/2)D3/2
A rod of height h is palced in a beaker of same radius. The height of the beaker is 3 times its radius. An observer sees the top end of the rod through a pin hole. When the beaker is filled with a liquid of refractive index √μ upto a height 2h, he can see the lower end of the rod. Find the value of μ
View SolutionA large vessel of height H is filled with a liquid of density ρ upto the brim. A small hole of radius r is made at the side vertical face, close to the base. The horizontal force is required to stop the gushing of liquid is
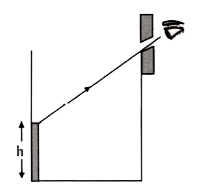
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
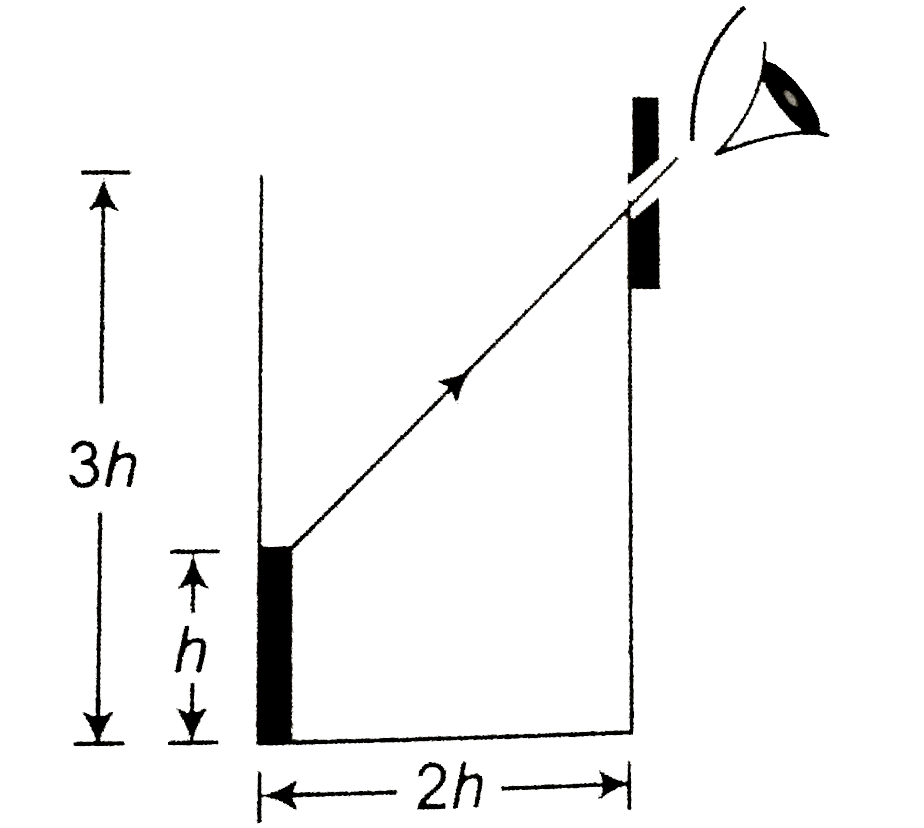
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View Solution
A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be moved
View Solution
