If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see figure), de-Broglie wavelength of electrons can be calculated by the relationship (n is an integer)
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
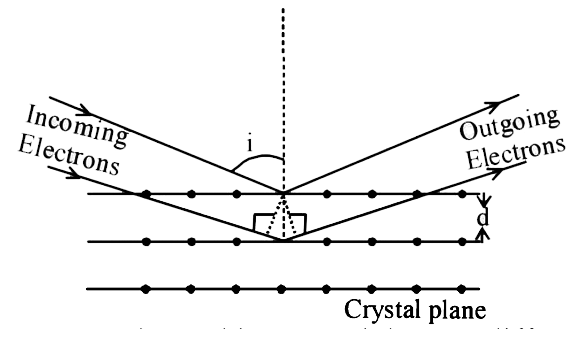
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
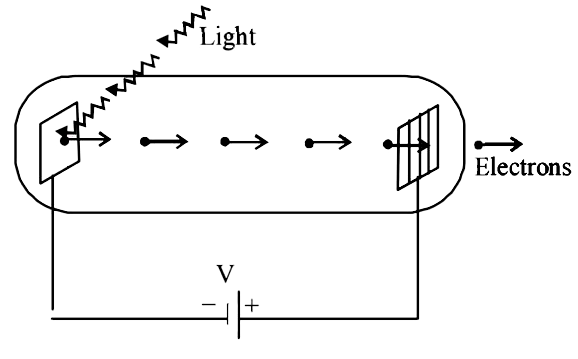
View SolutionLight of wavelength λphfalls on a cathode plate inside a vacuum tube as shown in the figure .The work function of the cathode surface is ϕ and the anode is a wire mesh of conducting material kept at distance d from the cathode. A potential different V is maintained between the electrodes. If the minimum de Broglie wavelength of the electrons passing through the anode is λe which of the following statement (s) is (are) true?
View Solution
Knowledge Check
Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely

If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)Adsini=nλdBB2dcosi=nλdBC2dsini=nλdBDdcosi=nλdBA metal plate is exposed to light with wavelength λ. It is observed that electrons are ejected from the surface of the metal plate. When a retarding uniform electric field E is imposed, no electron can move away from the plate farther than a certain distance d. Then the threshold wavelength λ0 for the material of plate is ( e is the electronic charge, h is Planck's constant and c is the speed of light)
AλeEd(eEd−hc)Bλhchc−eEdλCeEdλ−hchcλDλhc−eEdhcλThe electron of a H-atom moves in nth orbit. If the length of the orbit is L and de-Broglie wavelength is λ , then the relation between them is
AL=λ/nBλ=n/LCL=nλDL=nhλ
A monchromatic beam of electrons accelerated by a potential difference V falls normally on the plate containing two narrow slits seperated by a distance d. The interference pattern is observed on a screen parallel to the plane of the slit and at a distance of D from slits. Fringe width is found to be ω1. When electron beam is accelerated by the potential differene of 4V, the finge width becomes ω2. Find the ratio ω1ω2. (Given d<<D)
View SolutionA monchromatic beam of electrons accelerated by a potential difference V falls normally on the plate containing two narrow slits seperated by a distance d. The interference pattern is observed on a screen parallel to the plane of the slit and at a distance of D from slits. Fringe width is found to be ω1. When electron beam is accelerated by the potential differene of 4V, the finge width becomes ω2. Find the ratio ω1ω2. (Given d<<D)
View SolutionLight of wavelength λphfalls on a plate a vacum teke as shown in the figure .The work function of the conducting meterial kept at a distance d from the cathon A petential different V is maximum between the electrodes if the minimum de Brogle waveleeength of the electrons passing through the anode is λe which of the following statement (s) is (are) true?

View SolutionThe French physical Louis de Broglie in 1924 postulated that matter, like radiation, should exhibit a dual behaviour. He proposed the following relationship between the wavelength λ of a material particle, its linear momentum p and planck constant h.
λ=hp=hmv
The de Broglie relation implies that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than fighter particles.The wave associated with particles in motion are called matter waves or de Broglie waves.These waves differ from the electromagnetic waves as they
(I)have lower velocities
(II)have no electrical and magnetic fields and
(III)are not emitted by the particle under consideration
The experiment confirmation of the de Broglies relation was obtained when Davisson and Germer, in 1927, observed that a beam of electrons is diffrated by a nickel crystal.As diffraction is a characteristic property of waves hence the beam of electron behaves as a wave, as proposed by de broglie.
Using Bohr's theory, the transition, so that the electrons de-Broglie wavelength becomes 3 times of its orginial value in He+ ion will be
View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength .λ of a material particle,its linear momentum P and Planck constant h.
λ=hp=hmv
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, Δx and the uncertainty in the momentum Δ(mv) must be greater than or equal to h4π,i.e.,
ΔxΔ(mv)≥h4π
The transition so that the de Broglie wavelength of electron becomes 3 times of its initial value in He+ ion will be :
View Solution
