Three identical spheres each of radius R are placed touching side by side along X axis so that the centre of the first sphere is at the origin. Now the sphere at the extreme end is removed. The shift in the centre of mass is (A) R (B) 2R (C) R 2 (D) 3R
Step by step video & image solution for Three identical spheres each of radius R are placed touching side by side along X axis so that the centre of the first sphere is at the origin. Now the sphere at the extreme end is removed. The shift in the centre of mass is (A) R (B) 2R (C) R 2 (D) 3R by Physics experts to help you in doubts & scoring excellent marks in Class 13 exams.
Similar Questions
Three identical spheres each of radius 'R' are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is.
View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View Solution
Knowledge Check
- Question 1 - Select One
Three identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
A2R3B2RC5R3D4R3 - Question 2 - Select One
Three identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
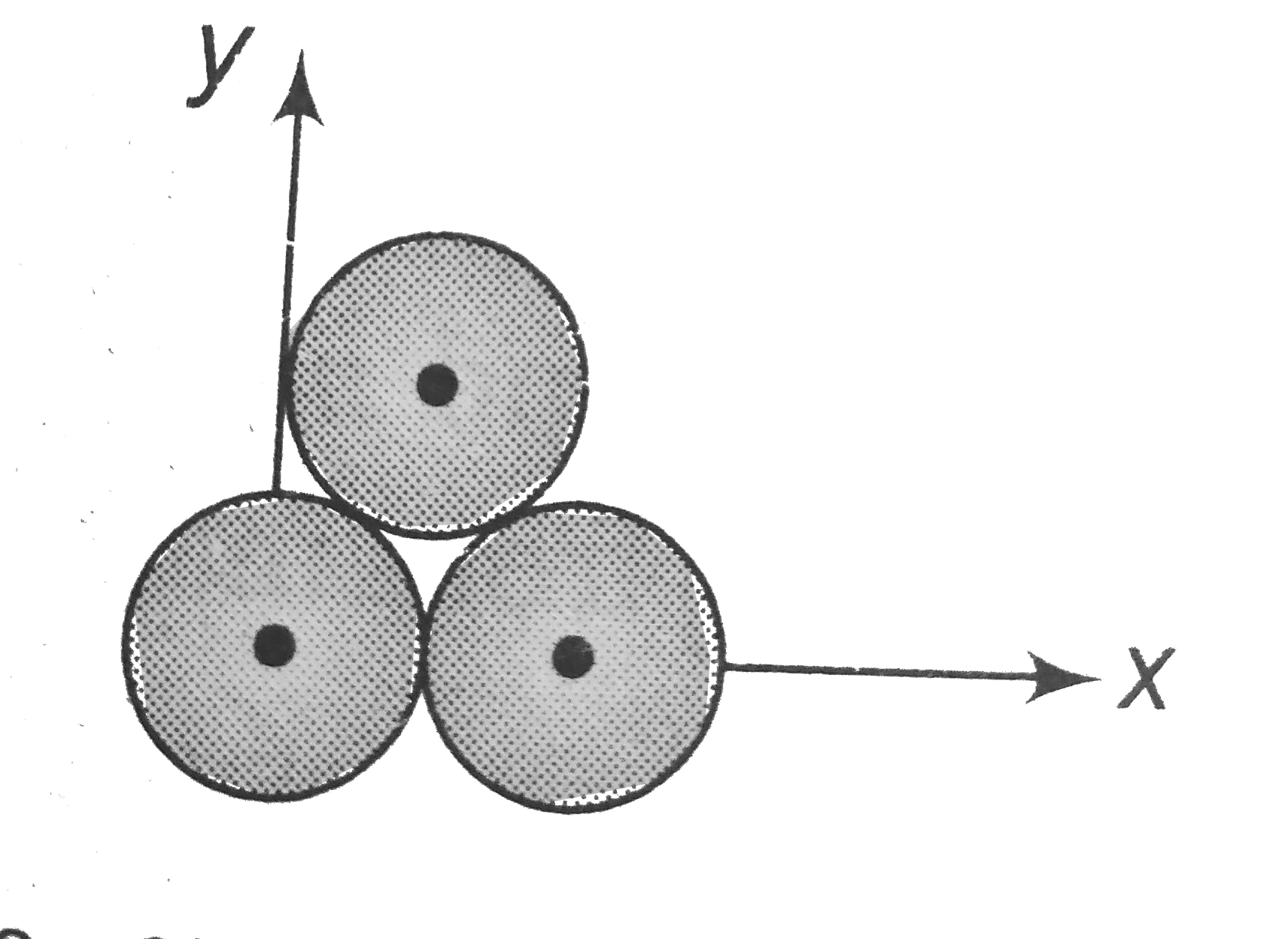 .A(R,R)B(0,0)C(R2,R2)D(R,R√3)
.A(R,R)B(0,0)C(R2,R2)D(R,R√3) - Question 3 - Select One
The volume of a sphere of radius 2r is
A32πr33B16πr33C8πr33D64πr33
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
View SolutionA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution
