Four persons are to be chosen at random from a group of 3 men, 2 women and 4 children. Find the probability of selecting: (i)1man 1woman and 2 children (ii)Exactly 2 children (iii) 2 women
Total persons=2+3+4=9
total ways=
1) favorable cases
2)Exactly 2 children
Case 1) 2 childdren 1 men 1 women
Case 2) 2 children 2 mean 0 women
Case 3) 2 children 0 mean 2 women
Total ways=
Case1)
Case2)
Case3)
.
Topper's Solved these Questions
Similar Questions
A family has 2 children. Find the probability that both are boys, if it is known that: (i) at least one of the children is a boy, (ii) the elder child is a boy.
View SolutionHow many diagonals does each of the following have?
(i) A convex quadrilateral
(ii) A regular hexagon
(iii) A triangleView SolutionFind the volume in cubic decimetre of each of the cubes whose side is (i)1.5m (ii) 75cm (iii) 2dm 5cm
View SolutionThe number of solutions of z2+¯z=0 is
(a) 1 (b)2
(c) 3 (d)4View SolutionThe number of integral pairs (x,y) satisfying the equation (x−y)2+2y2=27 is:
a. 8
b. 7
c. 6
d. 5View SolutionA box contains 3 blue, 2 white, and 4 red marbles. If a marble is drawn at random from the box, what is the probability that it will be(i) white? (ii) blue? (iii) red?
View SolutionDraw rough diagrams to illustrate the following: (i) Open curve (ii) Closed curve
View SolutionIn an AP, Sp=q, Sq=p. Then Sp+q is equal to:
a. 0
b. −(p+q)
c. (p+q)
d. pqView SolutionThe acute angle between the lines y=3 and y=√3x+k is
(A) 30° (B) 60° (C) 45° (D) 90°View SolutionFollowing are some figures: Classify each of these figures on the basis of the following:(i) Simple curve (ii) Simple closed curve (iii) Polygon (iv) Convex polygon (v)Concave polygon (vi) Not a curve
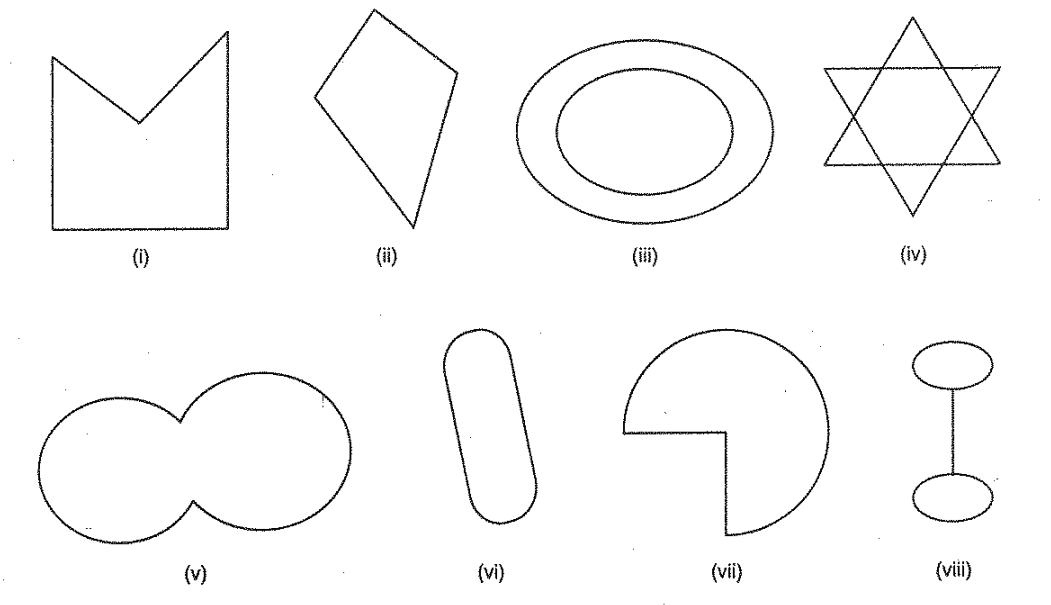 View Solution
View Solution

