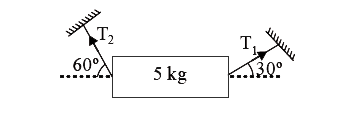A body of mass 5kg is suspended by the strings making angles 60∘ and 30∘with the horizontal -
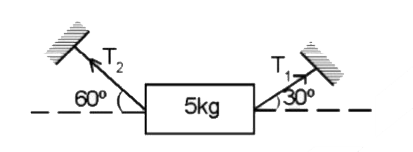
(a) T1=25N ( b) T2=25N
(c ) T1=25√3N (d) T2=25√3
a,b
a,d
c,d
b,c
The correct Answer is:B
Step by step video & image solution for A body of mass 5kg is suspended by the strings making angles 60^(@) and 30^(@)with the horizontal - (a) T_(1)= 25 N ( b) T_(2) = 25N (c ) T_(1) = 25 sqrt(3) N (d) T_(2) =25sqrt(3) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2
66 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2(Level-II)
25 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - SOLVED EXAMPLE
16 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
Knowledge Check
A body of mass 5 kg is suspended by the string making angles 60∘ and 30∘ with the horizontal
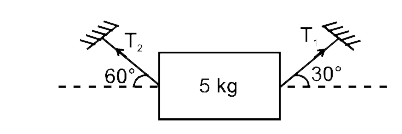
(a) T1=25N
(b) T2=25N
(c) T1=25√3N
(d) T2=25√3NAa, bBa, dCc, dDb, cA body of weight 2 kg is suspended as shown in the figure. The tension T1 in the horizontal string (in kg wt ) is
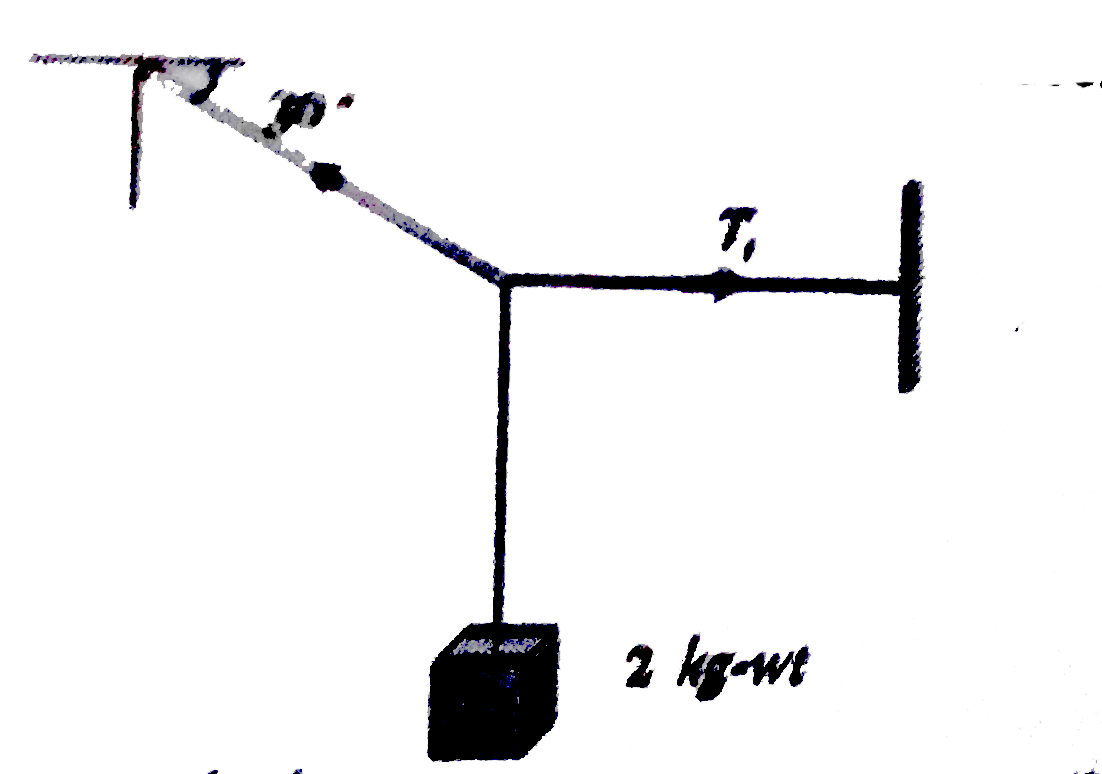 A2/√3B√3/2C2√3D2
A2/√3B√3/2C2√3D2In an A.P. if S1=T1+T2+T3+…+Tn (n odd) S2=T1+T3+T5+…+Tn, then S1/S2 =
A2nn+1Bnn+1Cn+12nDn+1n
limn−>∞2.5n+1−3.7n+12.5n+3.7n=
View SolutionIf (12−t1)+(22−t2)+......+(n2−tn)=13n(n2−1), then tn is
View SolutionIn fig tension in the string that connects the masses A and B is T1 and that in the string connecting B and C is T2 then T1T2 is:
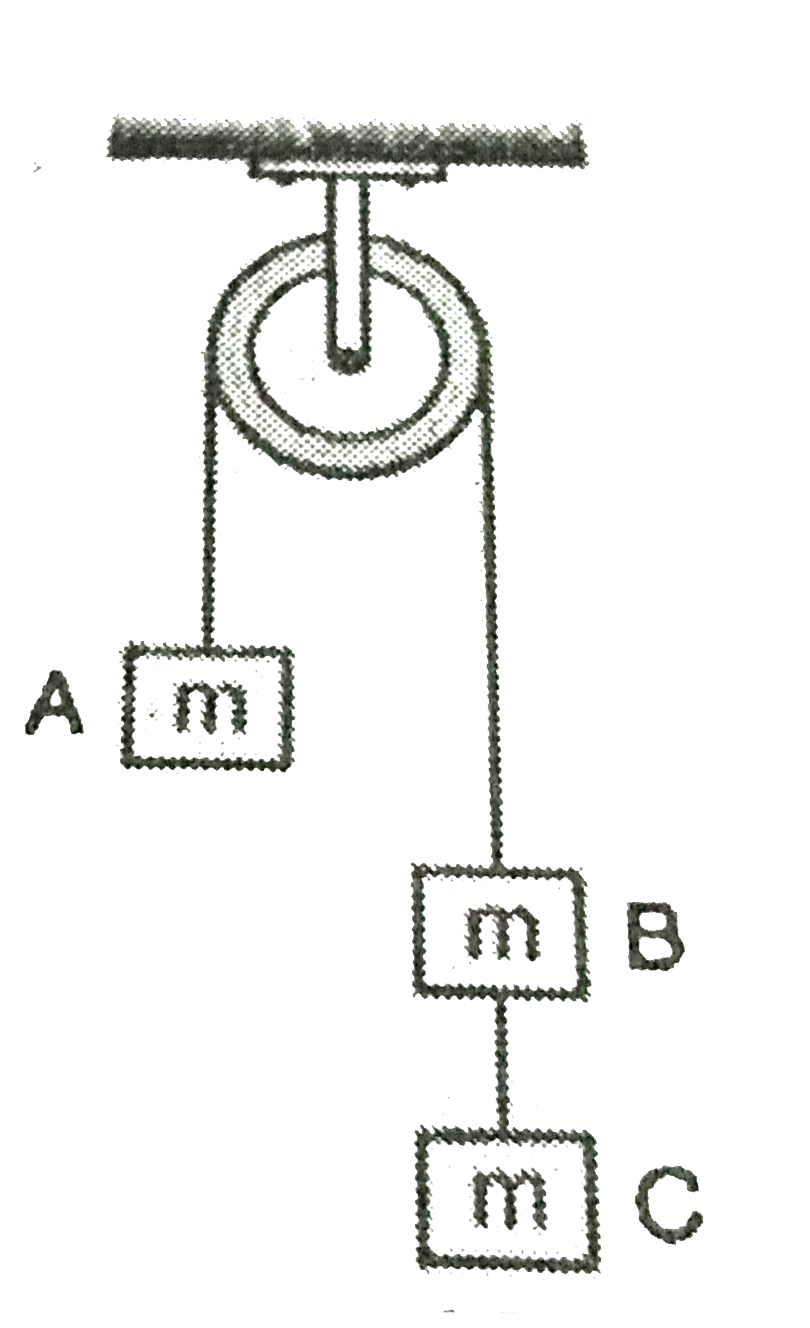
View SolutionIn the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?

View SolutionIf (12−t1)+(22−t2)++(n2−tn)+=n(n2−1)3 , then tn is equal to n2 b. 2n c. n2−2n d. none of these
View Solution