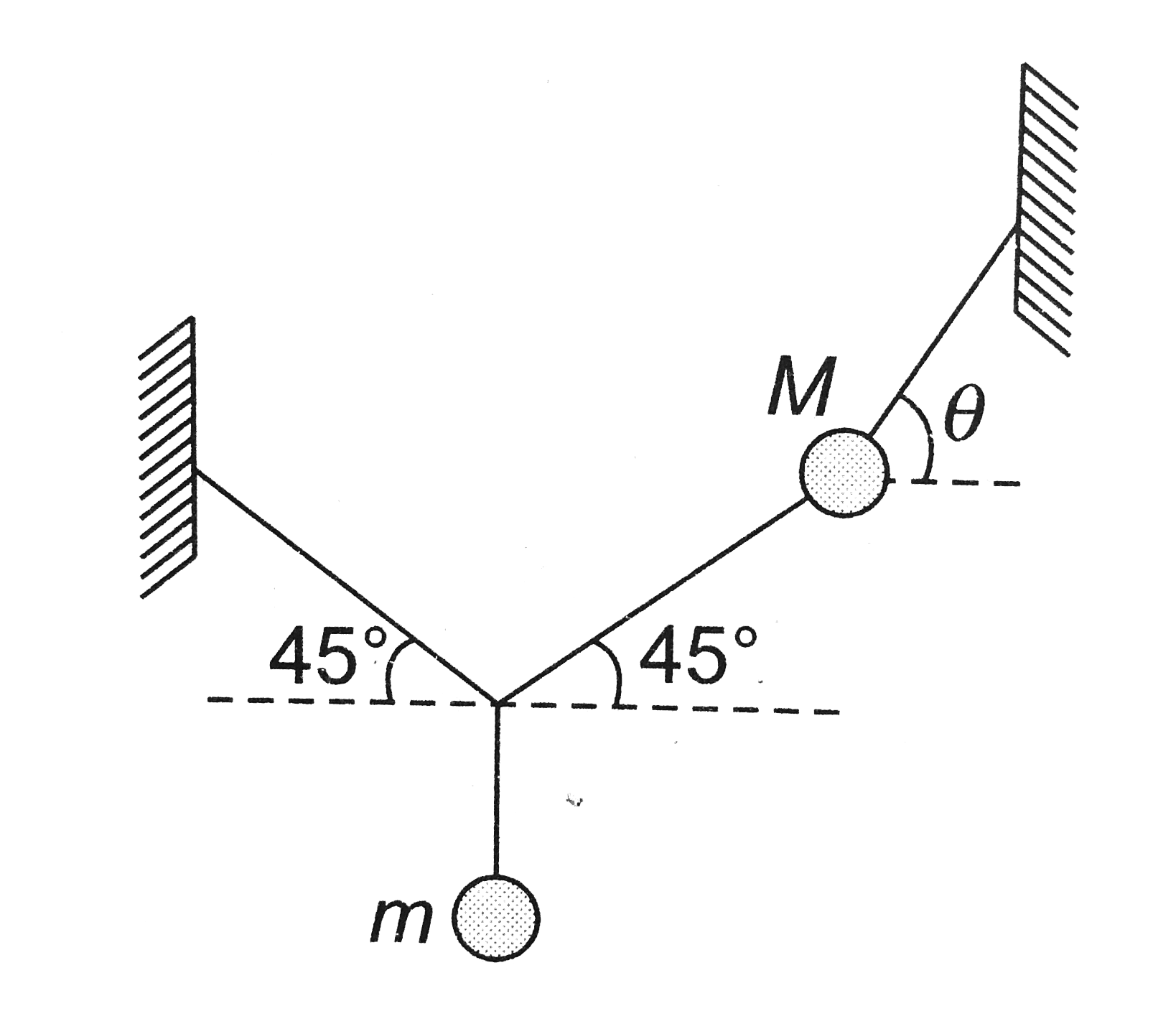
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then
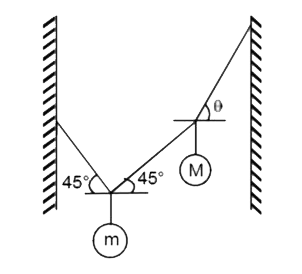
tanθ=1+2Mm
tanθ=1+2mM
cotθ=1+2Mm
cotθ=1+2mM
The correct Answer is:A
Step by step video & image solution for Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2(Level-II)
25 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-3(Level-I)
18 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCIS-1
80 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
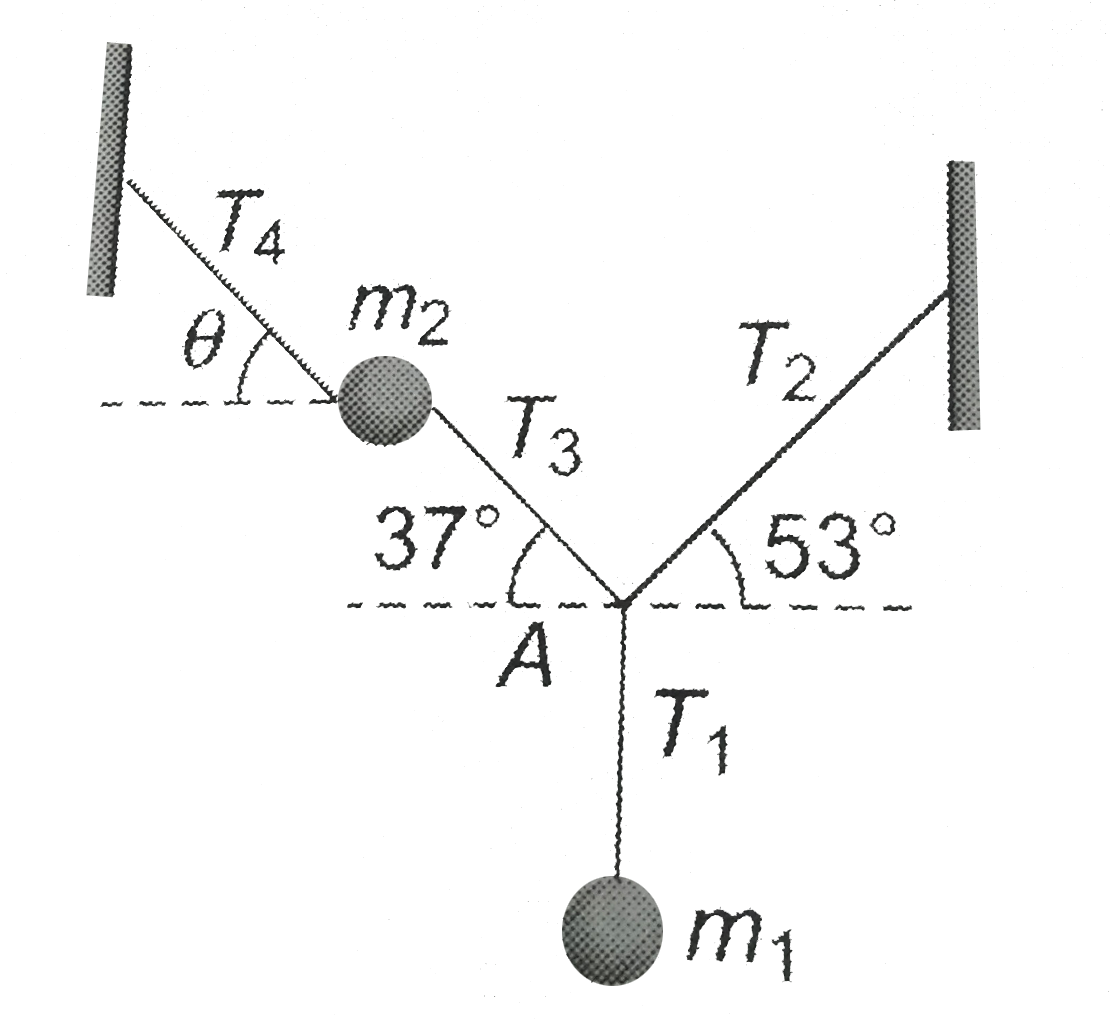
Two masses m1 and m2 are attached with light strings as shown. If the system is in equilibrium, find the value of θ
View SolutionA long rod ABC of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with A hinged at the bottom is
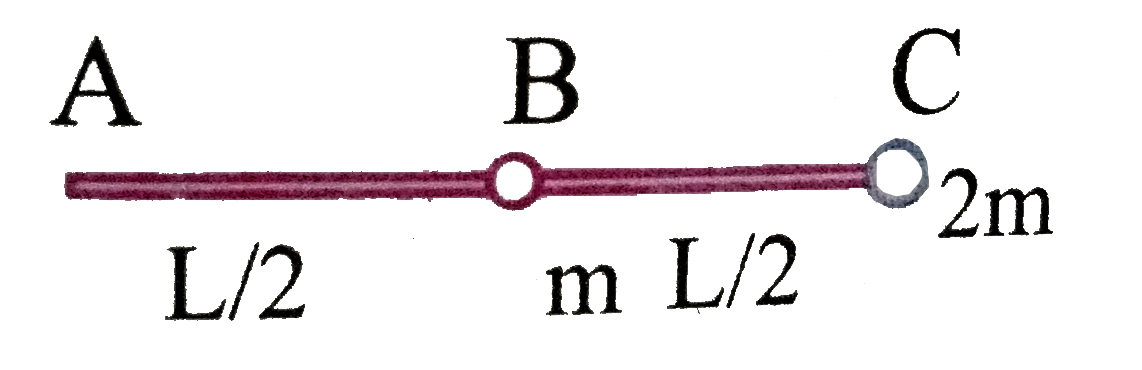 .
.
View Solution
Knowledge Check
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
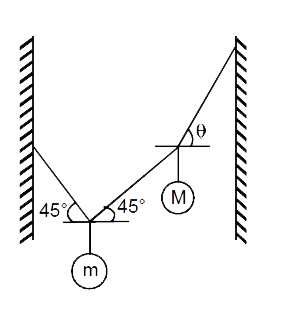 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mMTwo masses m and M are attached with strings as shown. For the system to be in equilibrium we have.
 Atanθ=1+2MmBtanθ=1+2mMCtanθ=1+M2mDtanθ=1+m2M
Atanθ=1+2MmBtanθ=1+2mMCtanθ=1+M2mDtanθ=1+m2MTwo bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
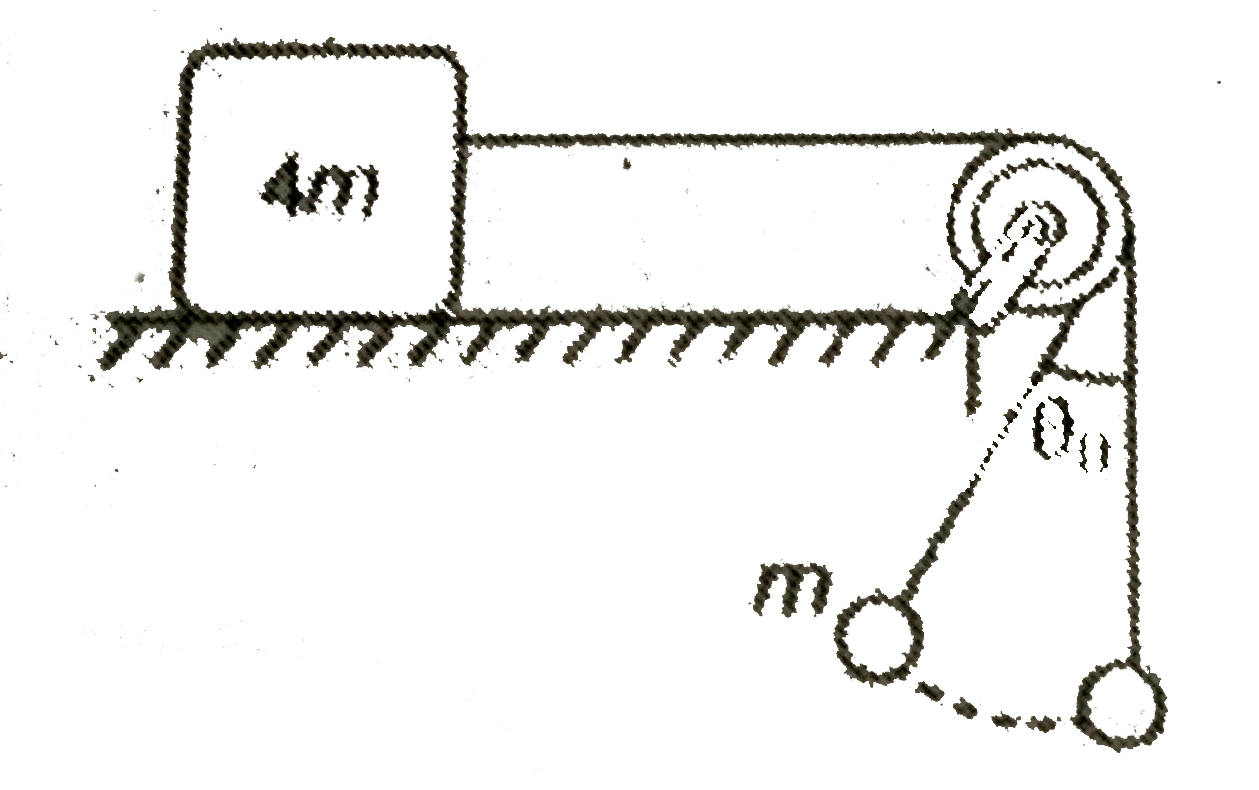 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
Two objects A and B of masses mA and mB are attached by strings as shown in fig. If they are given upward acceleration then the rato of tension T1:T2 is-
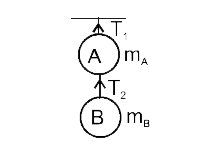
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
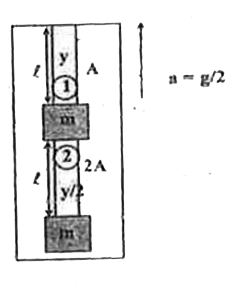
Ratio of elongation in rod 1 to that of rod 2 will be
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
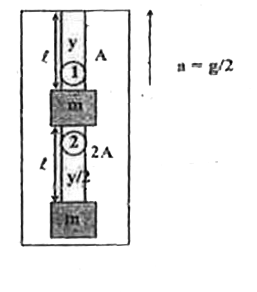
Ratio of PE stored in string-1 to string-2 in equilibrium is
View SolutionThe tension in the string shown in figure m−2m→F is.
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in Figure. If m1>m2 then the reading of spring balance will be
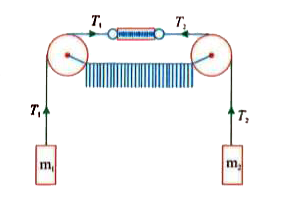
View Solution
