Two blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
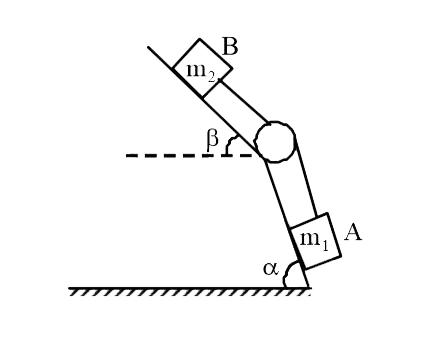
(m1sinα−m2sinβ)g
(m1+m2)(sinα−sinβ)g
m1m2gm1+m2(sinα+sinβ)
m1m2gm1+m2(sinα−sinβ)
The correct Answer is:D
Step by step video & image solution for Two blocks A and B of masses m_(1) and m, are connected by an inextensible string rest on two smooth planes inclined at angle alpha and beta as shown. The tension in string is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-2(Level-II)
Explore 25 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-3(Level-I)
Explore 18 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCIS-1
Explore 80 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 3 Section-B
Explore 12 Videos
- ONE DIMENSION MOTIONBook:MOTIONChapter:ONE DIMENSION MOTIONExercise:Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
Explore 12 Videos
Similar Questions
Two blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View Solution
Knowledge Check
Two blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively
 Ag,g/2Bg/2,gCg,gDg/2,g/2
Ag,g/2Bg/2,gCg,gDg/2,g/2Two blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively
 Ag,g2Bg2,gCg,gDg2,g2
Ag,g2Bg2,gCg,gDg2,g2Two blocks A and B of masses 3 m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively:
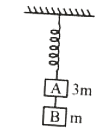 Ag,g3Bg,gCg3,g3Dg3,g
Ag,g3Bg,gCg3,g3Dg3,g
Two blocks of masses m1 = 3 kg and m2=1√3 kg are connected by a light inextensible string which passes over a smooth peg . The blocks rest on the inclined smooth planes of a wedge and the peg is fixed to the top of the wedge . The planes of the wedge supporting m1 and m2 are inclined at 30∘ and 60∘ respectively , with the horizontal. Calculate the acceleration of masses and the tension in the string .
View SolutionTwo masses 6 kg and 4 kg are connected by a flexible inextensible string rest on an inclined plane inclined at 60∘ with the horizontal as shown in figure. The coefficient of friction between the plane and the 6kg mass is 0.1 and the between the plane and the 4 kg massis 0.6 .
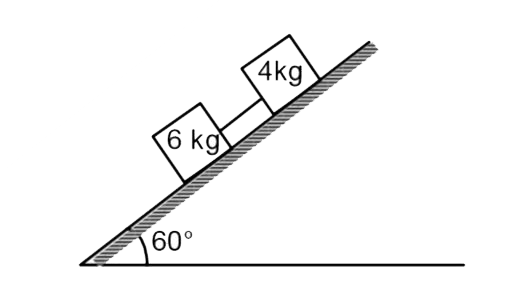
Find the tension in the connecting string.
View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

View SolutionThere blocks of masses m1 , m2 and m3 are connected by may less unstretchable strings on a smooth surface. Tension T2 is.
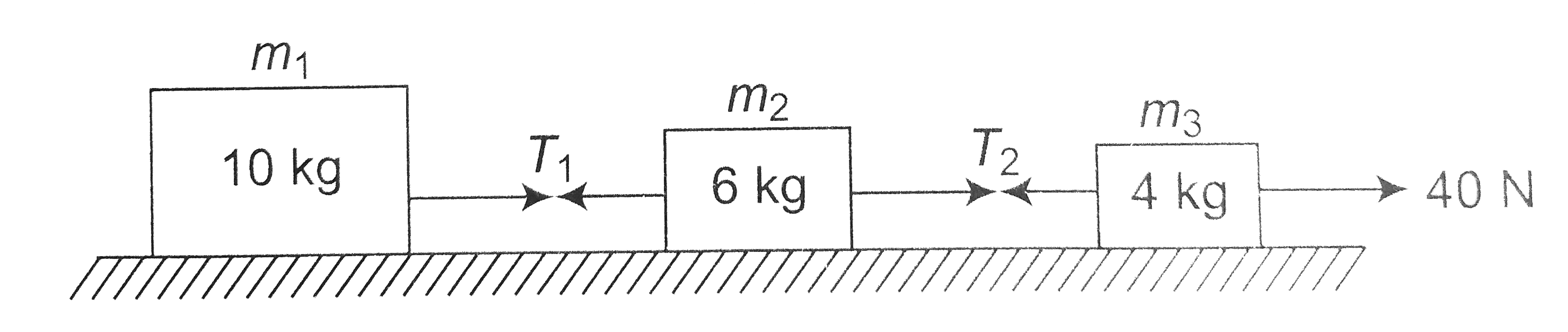
View Solution
