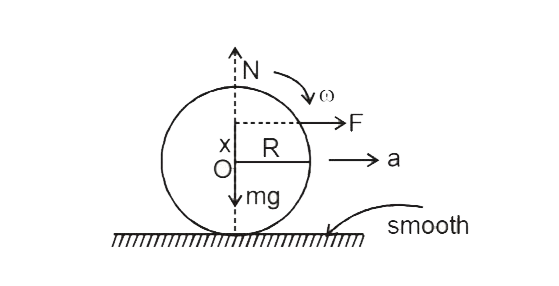
In a previous problem if force F applied at a distance x above the centre then find out linear and angular acceleation.
This force F translate the body linearly as well as rotate it. So,
Net toruqe about O it τ0=Fx
From rotational motion τ0=Iα
α=τl=Fx2MR23⇒α=3Fx2MR2
From linear of sphere
F = ma ⇒a=Fm
Topper's Solved these Questions
Similar Questions
Repeat the previous problem if the particle C s displaced through a distance x along the line AB.
View SolutionSuppose the rod in the previous problem has a mass of 1 kg distributed uniformly over its length.
a. find the initial angular acceleration of the rod.
b. Find the tension in the supports to the blocks of mass 2 kg and 5kg.
View Solution
Knowledge Check
A uniform thin flat isolated disc is floating in spece. It has radius R and mass m. A force F is applied to it a distanced =R2 from the centre in the y-direction Treat this problem as two-dimensional. At the instant shown the:
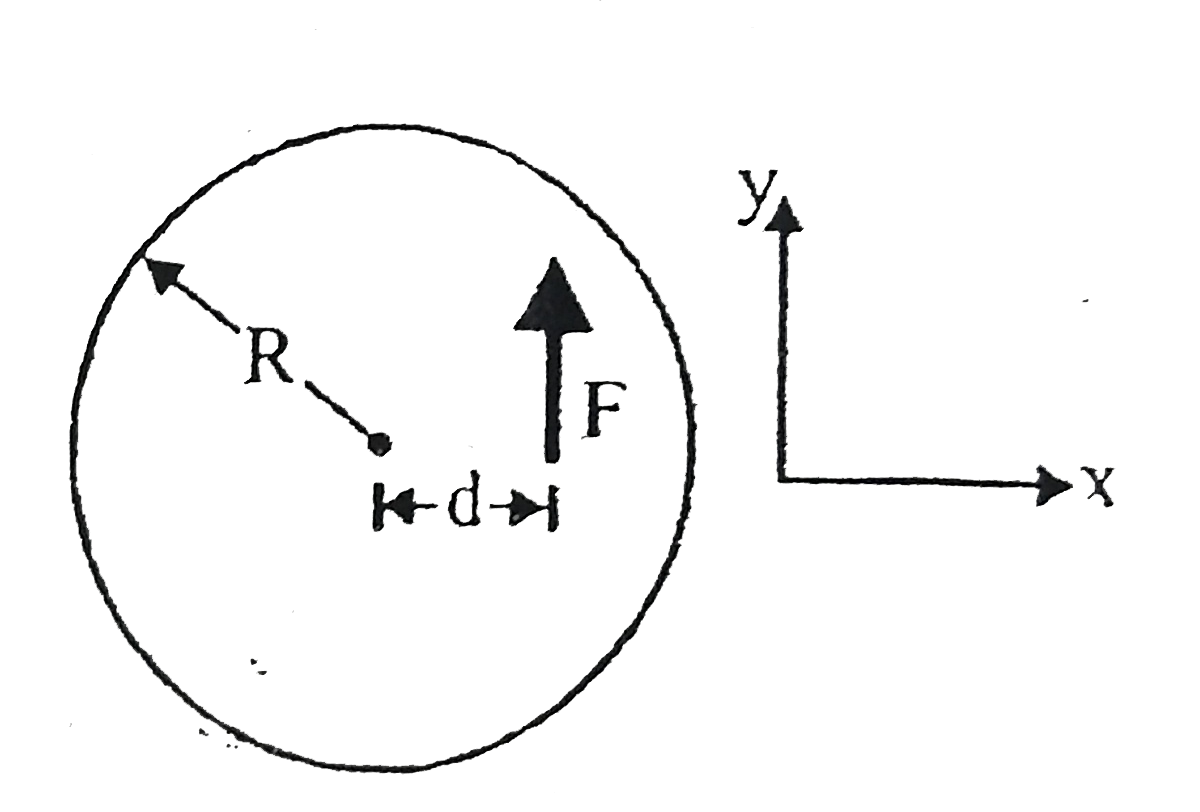 Aacceleration of the centre of the disc is f/mBangular acceleration of the disk is F/mRCacceleration of leftmost point on the disc is zeroDPoint which is instantaneously unaccelerated is the rightmost point.
Aacceleration of the centre of the disc is f/mBangular acceleration of the disk is F/mRCacceleration of leftmost point on the disc is zeroDPoint which is instantaneously unaccelerated is the rightmost point.A uniform thin flat isolated disc is floating in space. It has radius R and mass m . A force is applied to it at a distance d=(R2) from the centre in the y-direction. Treat this problem as two-dimensional. Just after the force is applied:
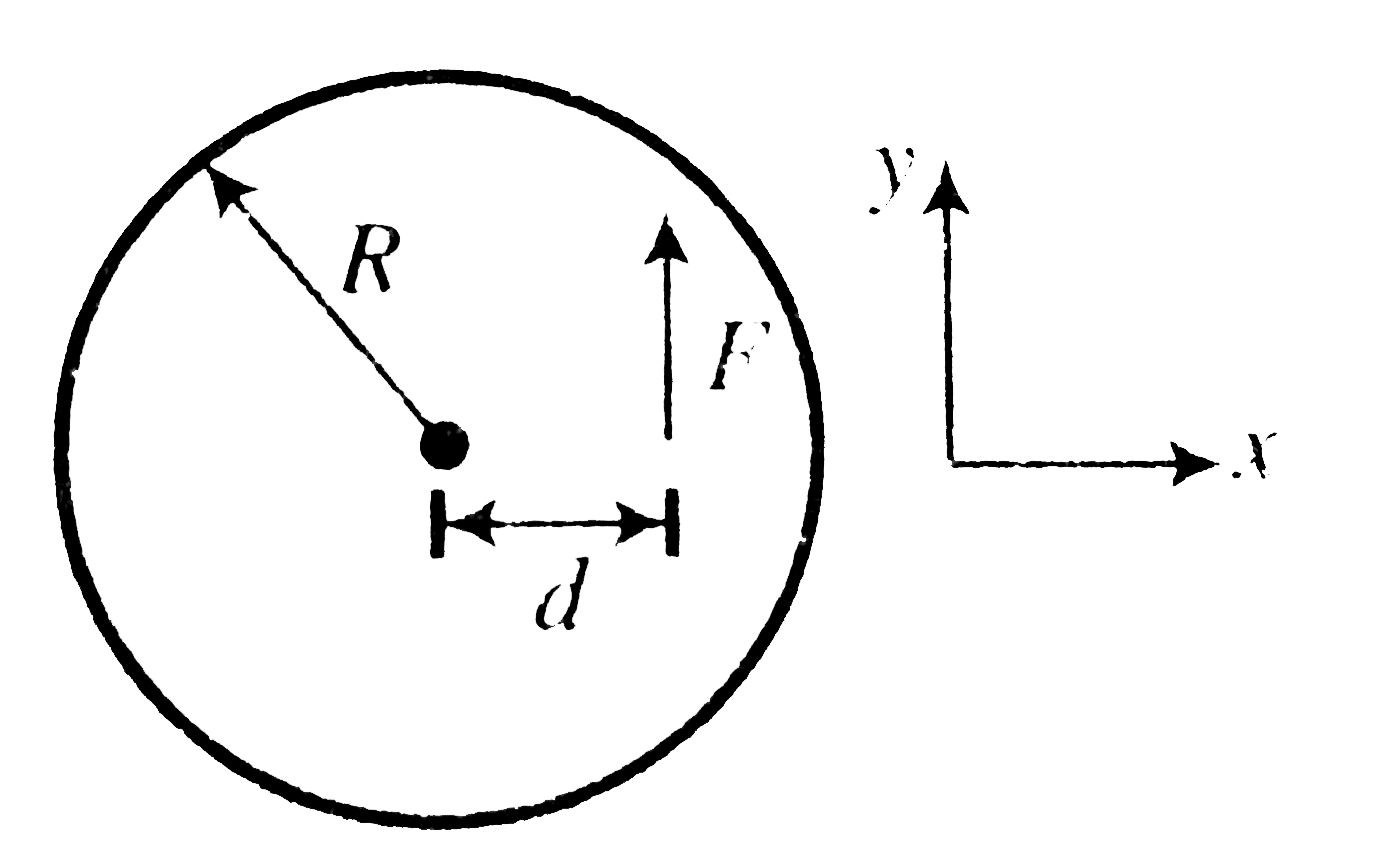 Aacceleration of the centre of the disc is F/m.Bangular acceleration of the disk is F/mR.Cacceleration of leftmost point on the, disc is zeroDpoint which is instantaneously unaccelerated is the rightmost point.
Aacceleration of the centre of the disc is F/m.Bangular acceleration of the disk is F/mR.Cacceleration of leftmost point on the, disc is zeroDpoint which is instantaneously unaccelerated is the rightmost point.The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
 AαA=αBBαA>αBCαA<αBDdata insufficient to determine
AαA=αBBαA>αBCαA<αBDdata insufficient to determine
In the previous problem. The friction force applied by ground on block B is
View SolutionA uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
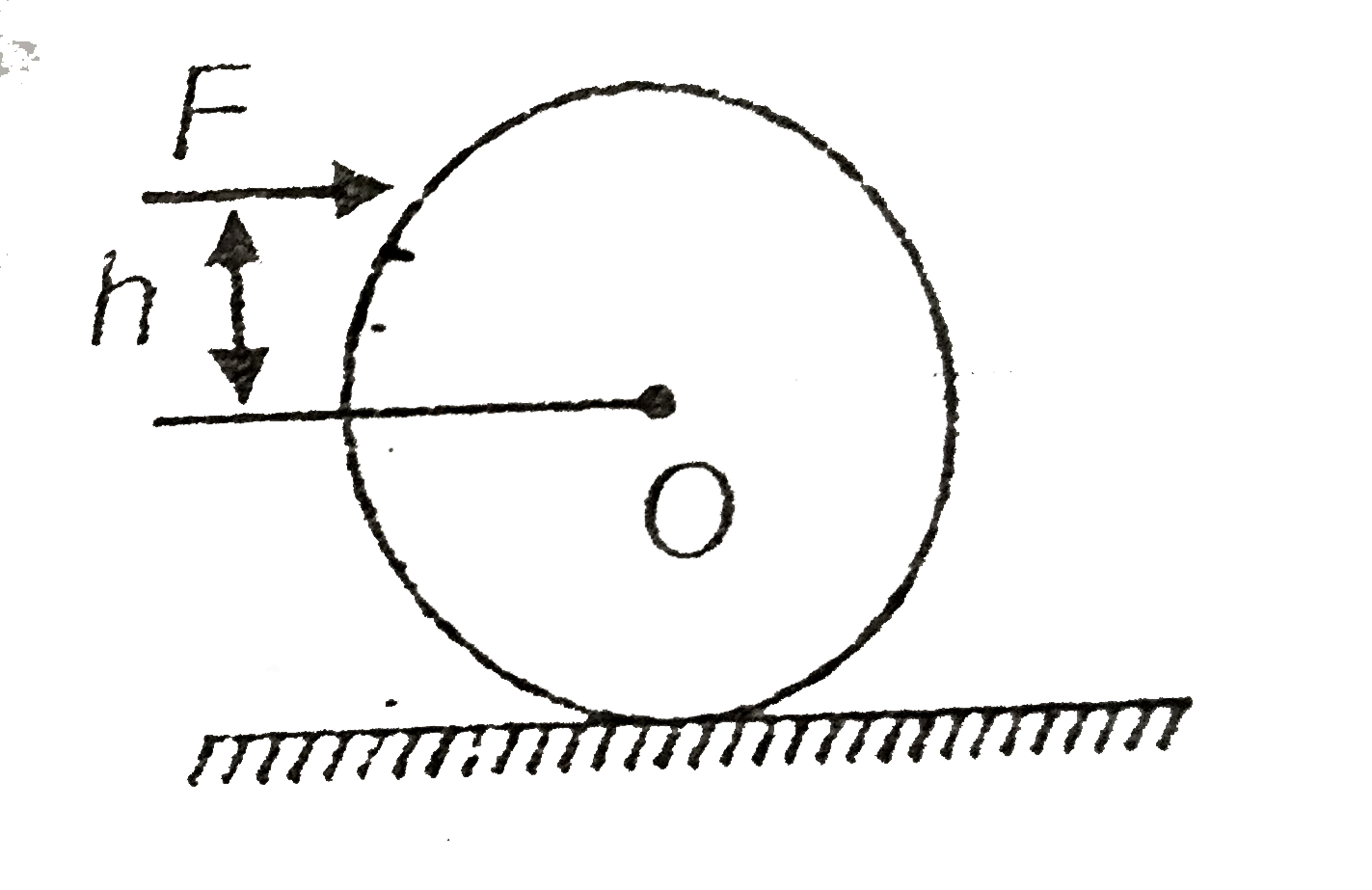
View SolutionA uniform sphere is place on a smooth horizontal surface and as horizontal force F is appied on it at a distance h above the surface. The acceleratioin of the centre
View SolutionIn the previous problem , if the applied force is made 20N , the acceleration of the upper and the lower blocks will be
View Solution
