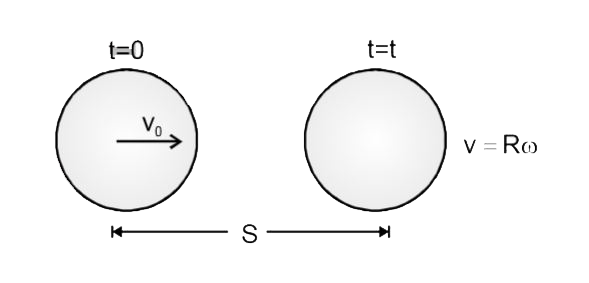
take rigid body a solid cylinder then find out the work done by friciton form time t = 0 to t = t (atv=rω)
Let us suppose that in between time t = 0 to t = t cylinder displaced s.
Translational work done by friciton + Rotational work Done by friciton
Now calculate each type of work done one by one
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find out one w.r.t. differentiation
ALoss of nucleus in seiveBDeath of protoplasm in tracheary elementsCCallus formationDLignification in vesselsFind out the one out w.r.t parasitic plants:
ACuscutaBViscumCRaffesiaDPisumThe displacement x of a particle at time t moving under a constant force is t=√x+3, x in metres, t in seconds. Find the work done by the force in the interval from t=0 to t=6 second.
A8JB4JC0JD6J
A body is acted upon by a force →F, given by
→F=−k[(cosωt)ˆi+(sinωt)ˆi] undergoes displacement, where the position vector
→r of the body is given by →r=a[cos(ωt+α)ˆi+sin(ωt+α)ˆj]. Find the work done by the force from time t=0 to time t=2π/ω.
View SolutionFind out the odd one w.r.t. role of potassium in plants.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View SolutionFind time period of the function, y=sinωt+sin2ωt+sin3ωt
View SolutionThe displacement of a body of mass 2 kg varies with time t as S=t2+2t, where S is in m and t is in s. The work done by all the forces acting on the body during the time interval t=2 to t=4 s is
View Solution
