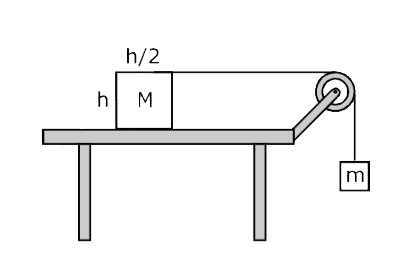
A cylinder of height h, diameter h//2 and mass M and with a homogene

Two masses $m_{1}$ and $m_{2}$ are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming $m_{1} > m_{2}$ acceleration of the system is:

A $\frac{m_{1} g {sin θ}_{1} + m_{2} g {sin θ}_{2}}{m_{1} + m_{2}}$
B $\frac{m_{1} g {sin θ}_{1} - m_{2} g {sin θ}_{2}}{m_{1} - m_{2}}$
C $\frac{m_{1} g {sin θ}_{1} - m_{2} g {sin θ}_{2}}{m_{1} + m_{2}}$
D $\frac{(m_{1} + m_{2}) ({sin θ}_{1} + {sin θ}_{2}) g}{m_{1} - m_{2}}$
In the following figure, a body of mass m is tied at one end of a light string and this string is wrapped around the solid cylinder of mass M and radius R. At the moment t = 0 the system starts moving. If the friction is negligible, angular velocity at time t would be

A $\frac{m g R t}{(M + m)}$
B $\frac{2 M g t}{(M + 2 m)}$
C $\frac{2 m g t}{R (M - 2 m)}$
D $\frac{2 m g t}{R (M + 2 m)}$
A uniform horizontal metre scale of mass m is suspended by two vertical strings attached to its two ends. A body of mass 2m is placed on the 75 cm mark. The tensions in the two strings are in the ratio is
A $1 : 2$
B $1 : 3$
C $2 : 3$
D $3 : 4$

The correct Answer is:1/4