Consider the system shown below. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM.
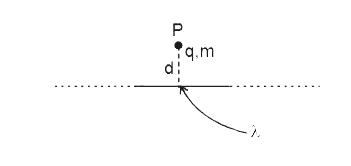
: At equilbrium position weight of the particle is balanced by the electric force
⇒mg=qE
mg=q2kλd ...(1)
Now if the particle is slightly displaced by a distance xλ (where x<<d ) net force on the body,
Fnet2kλqd+x−mg
from (1)
Fnet=2kλqd+x−2kλqd=−2kλqxd(d+x)
x<<dFnet≈−2kλqxd2
⇒a=−−2kλqxmd2
for SHM
a=−ω2x
∴−ω2=2kλqmd2
⇒ω=√2kλqmd2
T=2πω=2π√md22kλq
Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)
10 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)
10 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
Knowledge Check
A light inextensible string carrying a springs is passed over two smooth fixed pulles as shown. If the rod is slightly displaced about the hinge form is equilibrium position, then time period is.
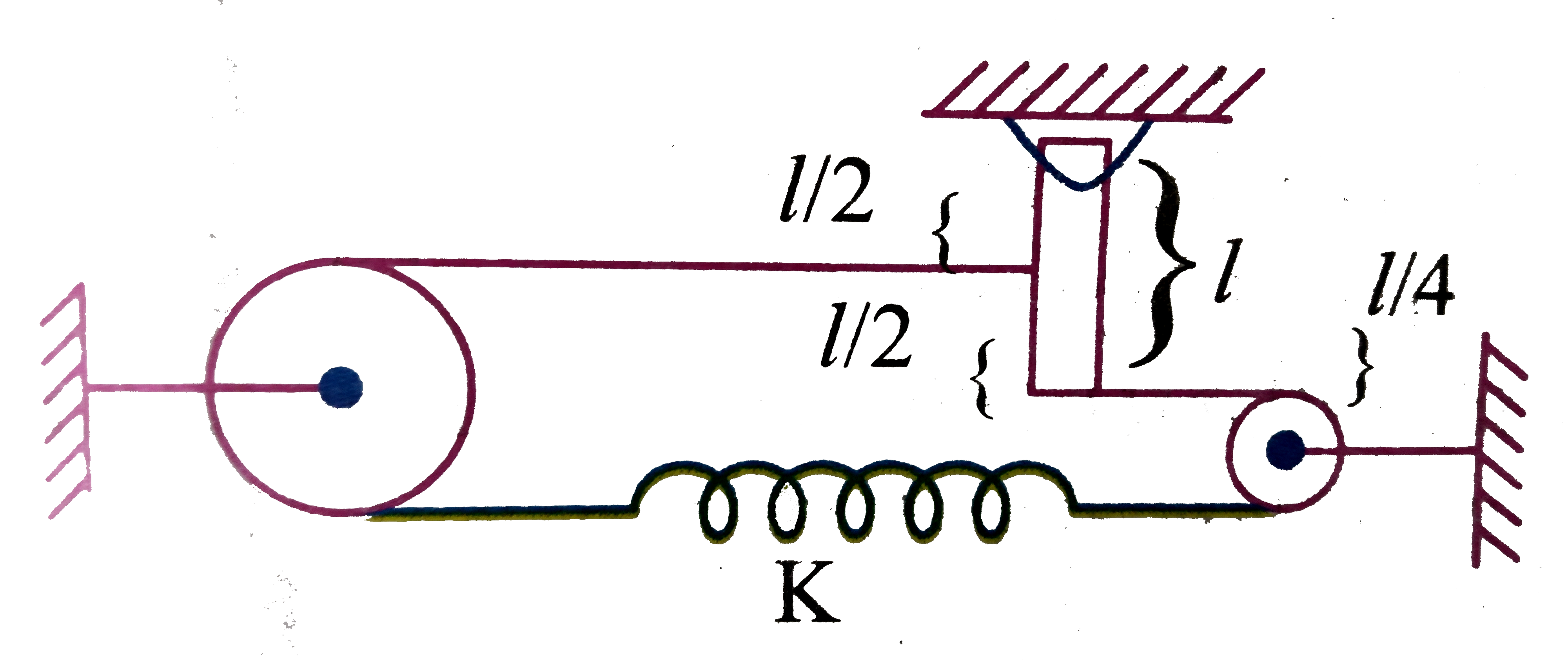 Aπ√4ml3(kl+2mg)+π√2l3gBπ√2mlkl+2mg+π√2l3Cπ√3mlkl2mg+π√l3Dπ√4mlml+2mg+π√l3
Aπ√4ml3(kl+2mg)+π√2l3gBπ√2mlkl+2mg+π√2l3Cπ√3mlkl2mg+π√l3Dπ√4mlml+2mg+π√l3Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
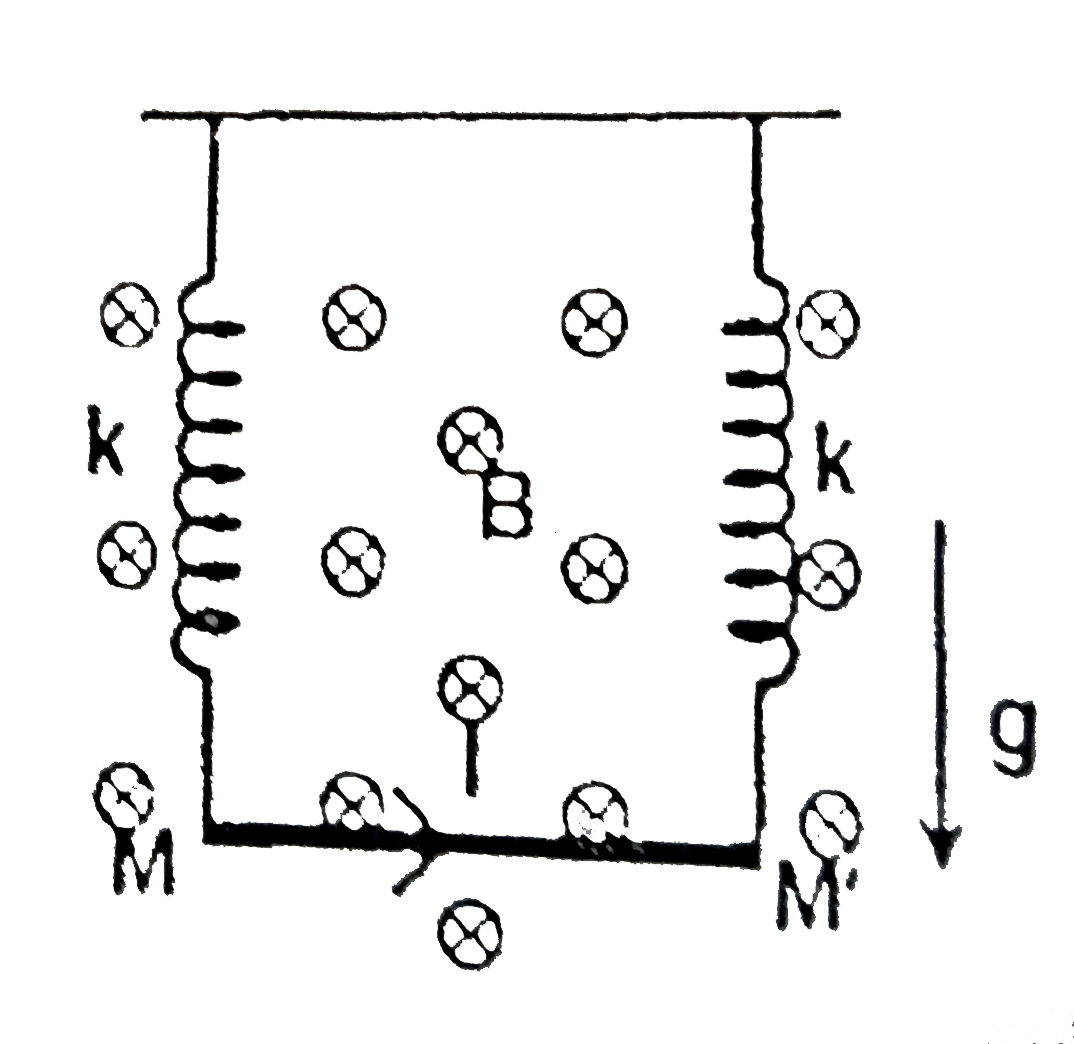 A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

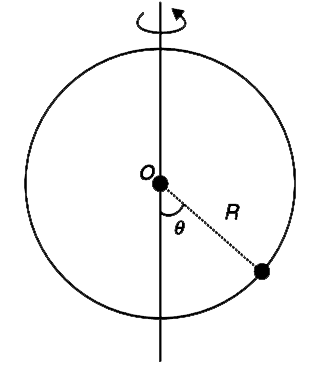
View SolutionA circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
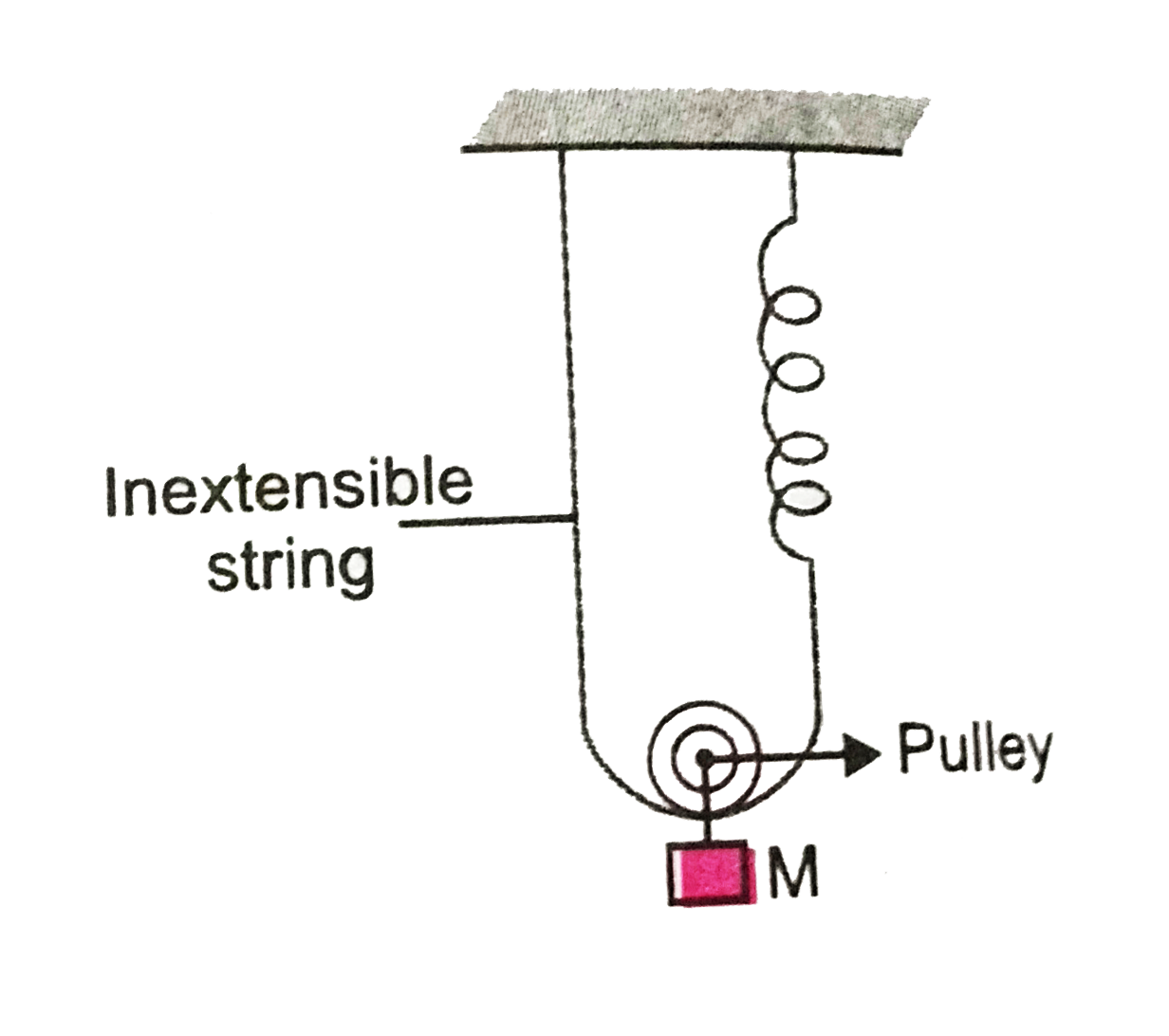
View SolutionThe time period of system shown below is :-
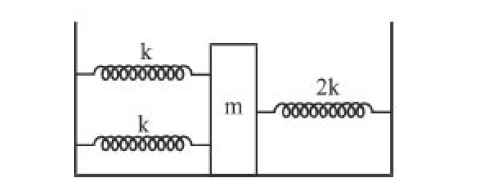
View Solution
