Calculate the work done to displace the particle from
(1,2) to (4,5) .if $\to F = 4 ˆ i + 3 ˆ j$

Video Solution

Text Solution

Verified by Experts

$d w = \to F . d \to r (d \to r = d x ˆ i + d y ˆ j + d z ˆ k)$
$d w = (4 ˆ i + 3 ˆ j) . (d x ˆ i + d y ˆ j + d z ˆ k)$
$\Rightarrow d w = 4 d x + 3 d y$
$\int_{0}^{w} d w = \int_{1}^{4} 4 d x + \int_{2}^{5} 3 d y$
$\Rightarrow w = {[4 x]}_{1}^{4} + {[3 y]}_{2}^{5}$
$w = (16 - 4) + (15 - 6)$
$\Rightarrow w = 12 + 9 = 21$ Joule
II format : (When F is given as a function of x, y, z)
If $\to F = F_{x} ˆ i + F_{y} ˆ j + F_{z} ˆ k$
then
$d w = (F_{x} ˆ i + F_{y} ˆ j + F z ˆ k) . (d x ˆ i + d y ˆ j + d z ˆ k)$
$\Rightarrow d w = F_{x} d x + F_{y} d y + F z d z$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Constant forces $P_{1} = ˆ i - ˆ j - ˆ k, P_{a} = - ˆ i + 2 ˆ j - ˆ k$ and $P_{3} = ˆ j - ˆ k$ act on a particle at a point A. The work done when the particle is displaced from the point A to B, where $A = 4 ˆ i - 3 ˆ j - 2 ˆ k$ and $B = 6 ˆ i + ˆ j - 3 ˆ k$ is
A3
B9
C20
DNone of these
Question 2 - Select One
A force of $\to F = 2 x ˆ i + 2 ˆ j + 3 z^{2} ˆ k N$ is acting on a particle. Find the work done by this force in displacing the body from $(1, 2, 3) m$ to $(3, 6, 1) m$ .
A(a) $- 10 J$
B(b) $100 J$
C(c) $10 J$
D(d) $1 J$
Question 3 - Select One
A force $\to F = (3 x y - 5 z) ˆ j + 4 z ˆ k$ is applied on a particle. The work done by the force when the particle moves from point $(0, 0, 0)$ to point $(2, 4, 0)$ as shown in figure.

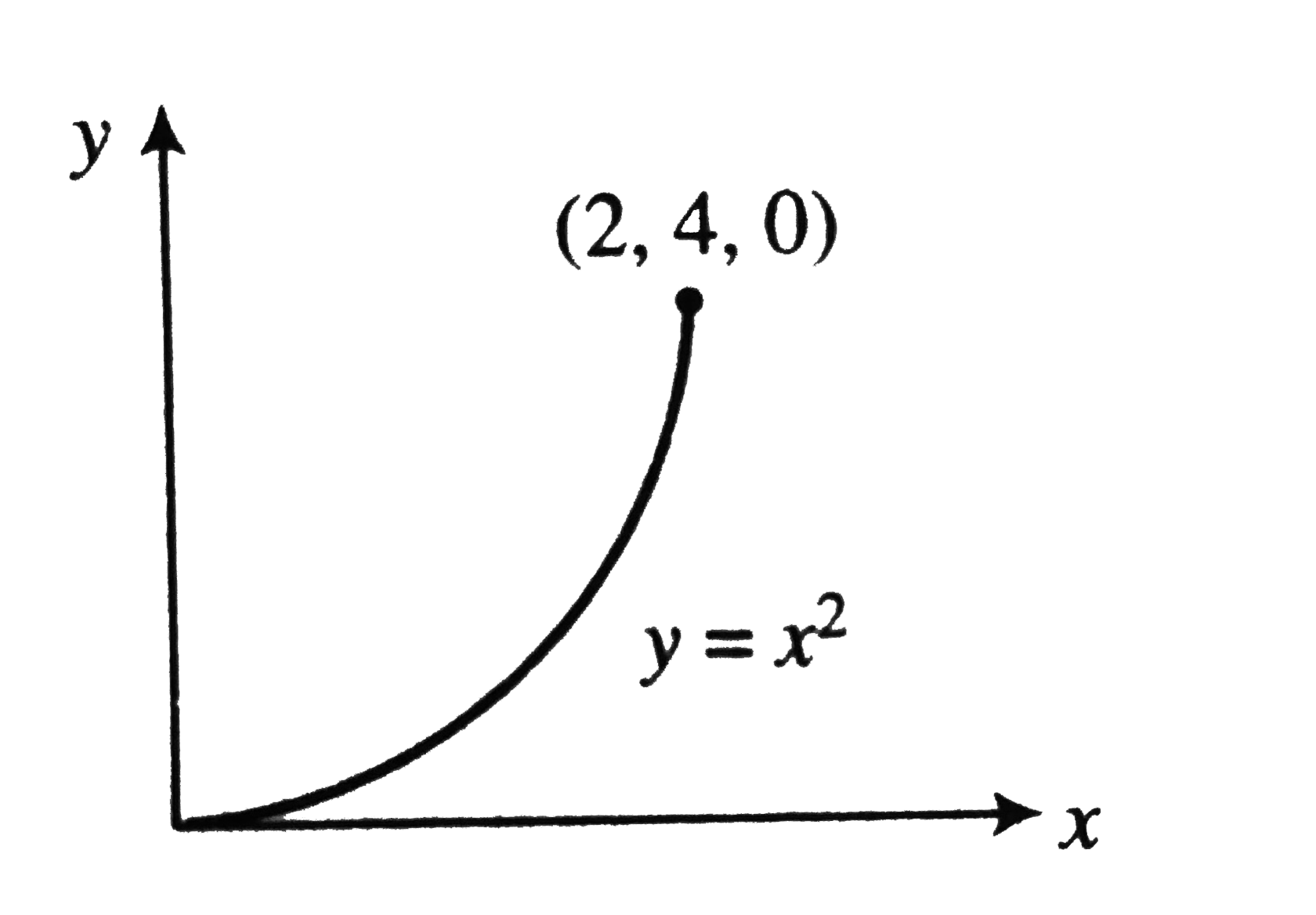A(a) $\frac{280}{5} u n i t s$
B(b) $\frac{140}{5} u n i t s$
C(c) $\frac{232}{5} u n i t s$
D(d) $\frac{192}{5} u n i t s$

MOTION-ELECTROSTATICS - I -EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED

Home
Ask Doubt
Profile