Two small identical balls P and Q, each of mass 0.866 g, carry identical charges and are suspended by two threads of equal length 50 cm each from the same point. At equilibrium, they are separated by a distance of 50 cm. Find the charge on each ball (in nearest integer in $n C$ ).

Video Solution

Text Solution

Verified by Experts

The correct Answer is:373

Answer

Step by step video, text & image solution for Two small identical balls P and Q, each of mass 0.866 g, carry identical charges and are suspended by two threads of equal length 50 cm each from the same point. At equilibrium, they are separated by a distance of 50 cm. Find the charge on each ball (in nearest integer in nC). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two small spherical balls each carrying a charge $Q = 10 μ C$ ( 10 micro=coulomb) are suspended by two insulating threads of equal lengths $1 c m$ each, from a point fixed in the ceiling. It is found that in equilibrium threads are sepreated by an angle $60^{\circ}$ between them, as shown in figure. What is the tension in the threads
(Given $\frac{1}{4 π ε_{0}} = 9 \times 10^{9} N m / C^{2}$ )

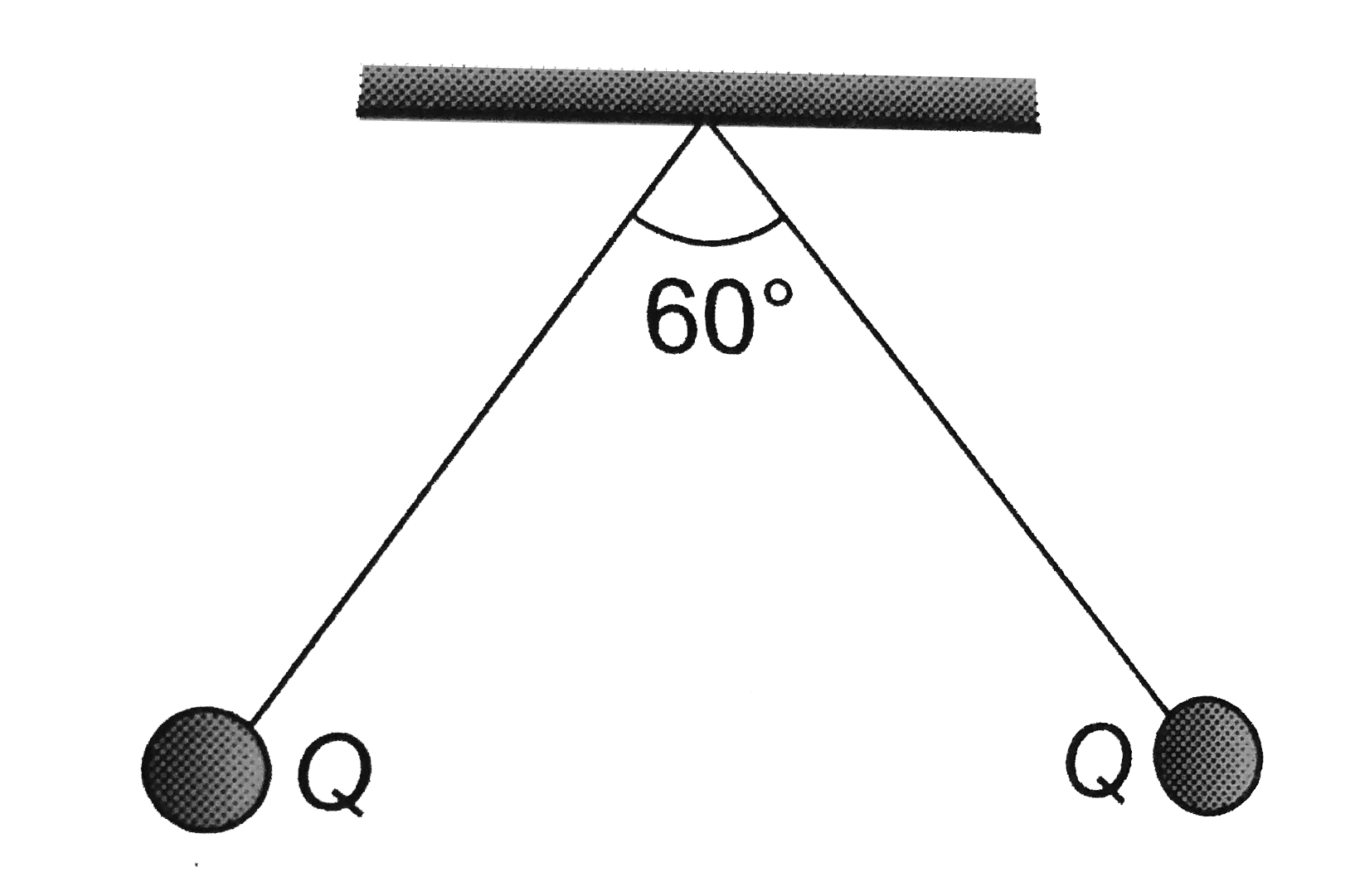A $18 N$
B $1.8 N$
C $0.18 N$
DNone of the above
Question 2 - Select One
Two small balls, each having equal positive charge $Q$ are suspended by two insulation strings of equal length $l$ from a hook fixed to a stand. It mass of each ball $= m$ and total angle between the two strings is $60^{\circ}$ m, then find the charge on each ball.

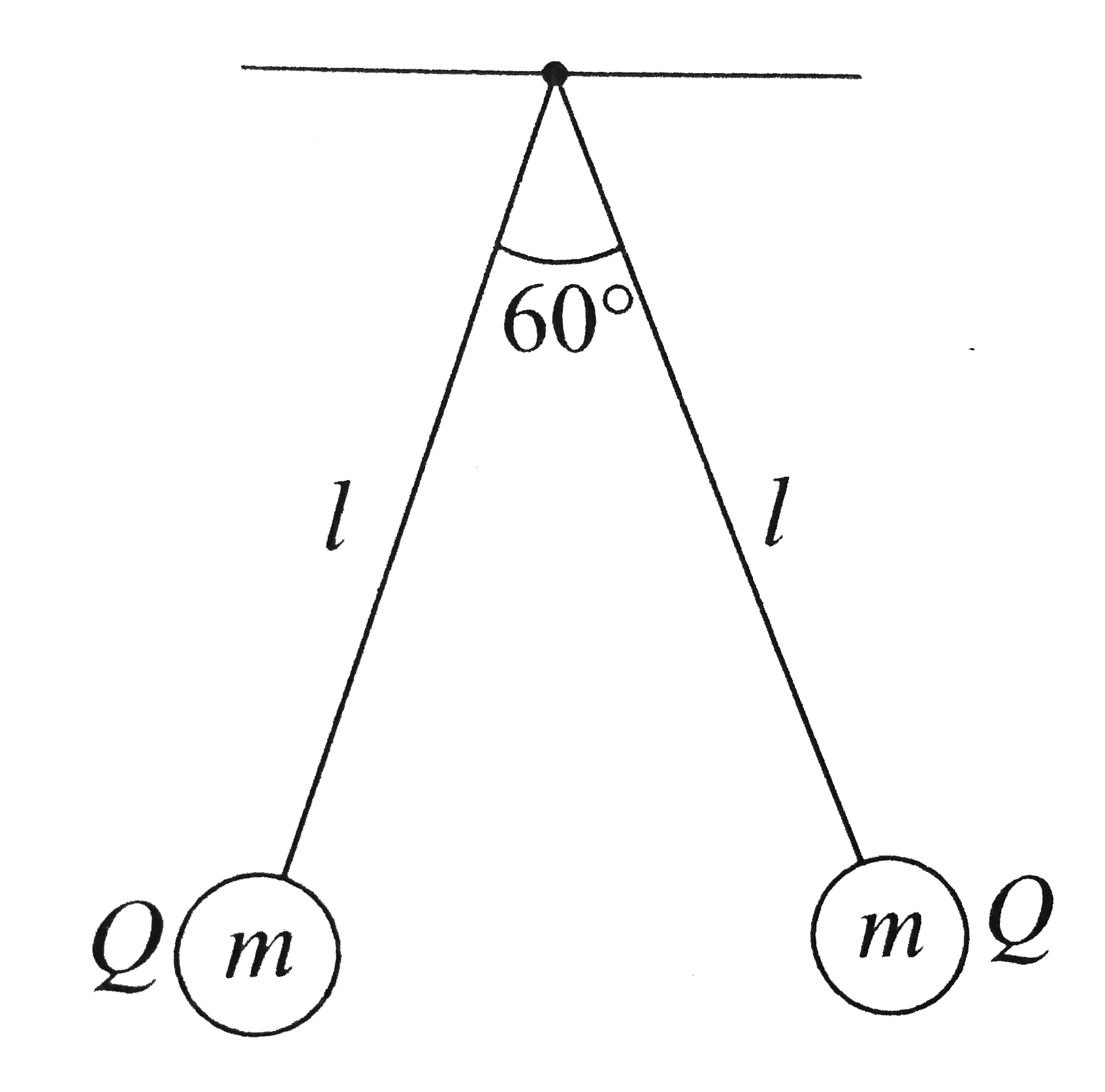A $\sqrt{\frac{m g}{4 π ε_{0} l^{2}}}$
B $\sqrt{2 π ε_{0} l^{2} m g}$
C $\sqrt{\frac{π ε_{0} l^{2} m g}{4}}$
D $\sqrt{\frac{4 π ε_{0} l^{2} m g}{\sqrt{3}}}$
Question 3 - Select One
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$

MOTION-ELECTROSTATICS - I -EXERCISE - 3 (Level -I) (Section A)

Home
Ask Doubt
Profile

Two small identical balls P and Q, each of mass 0.866 g, carry identical charges and are suspended by two threads of equal length 50 cm each from the same point. At equilibrium, they are separated by a distance of 50 cm. Find the charge on each ball (in nearest integer in nC).

The correct Answer is:373

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two small balls, each having equal positive charge Q are suspended by two insulation strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.

Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?

MOTION-ELECTROSTATICS - I -EXERCISE - 3 (Level -I) (Section A)

Two small identical balls P and Q, each of mass 0.866 g, carry identical charges and are suspended by two threads of equal length 50 cm each from the same point. At equilibrium, they are separated by a distance of 50 cm. Find the charge on each ball (in nearest integer in $n C$ ).

Two small balls, each having equal positive charge $Q$ are suspended by two insulation strings of equal length $l$ from a hook fixed to a stand. It mass of each ball $= m$ and total angle between the two strings is $60^{\circ}$ m, then find the charge on each ball.

Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?