two concentric rings of radii r and 2rare placed with centre at origin. Tow charges +q each are fixed at the diametrically opposite points of the rings as shown in figure . Smaller ring is now rotated by an angle 90∘ about Z-axis then it is again rotated by 90∘ about Y-axis . Find the work done by electrostatic forces in each step . If finally larger ring is rotated by 90∘ about X-axis , find the total work required to perform all three steps .
.
The correct Answer is:Wfist step=(83−4√5)Kq2r,Wsecond step=0,Wtotal=0
Step by step video & image solution for two concentric rings of radii r and 2rare placed with centre at origin. Tow charges +q each are fixed at the diametrically opposite points of the rings as shown in figure . Smaller ring is now rotated by an angle 90^@ about Z-axis then it is again rotated by 90^@ about Y-axis . Find the work done by electrostatic forces in each step . If finally larger ring is rotated by 90^@ about X-axis , find the total work required to perform all three steps . . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 3 (Level -II) (Section F)2videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -I) PREVIOUS YEAR - JEE MAIN21videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 3 (Level -II) (Section C)4videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main30videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)30videos
ELECTROSTATICS-II
Similar Questions
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
View SolutionMoment of inertia of a ring about its diametric axis is l. Two such rings are welded as shown in figure. The new moment of inertia about XX' ais is
_PHY_204_Q01.png)
View Solution
Knowledge Check
- Question 1 - Select One
Two identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
A3MR2B32MR2C14MR2D2MR2 - Question 2 - Select One
Three rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
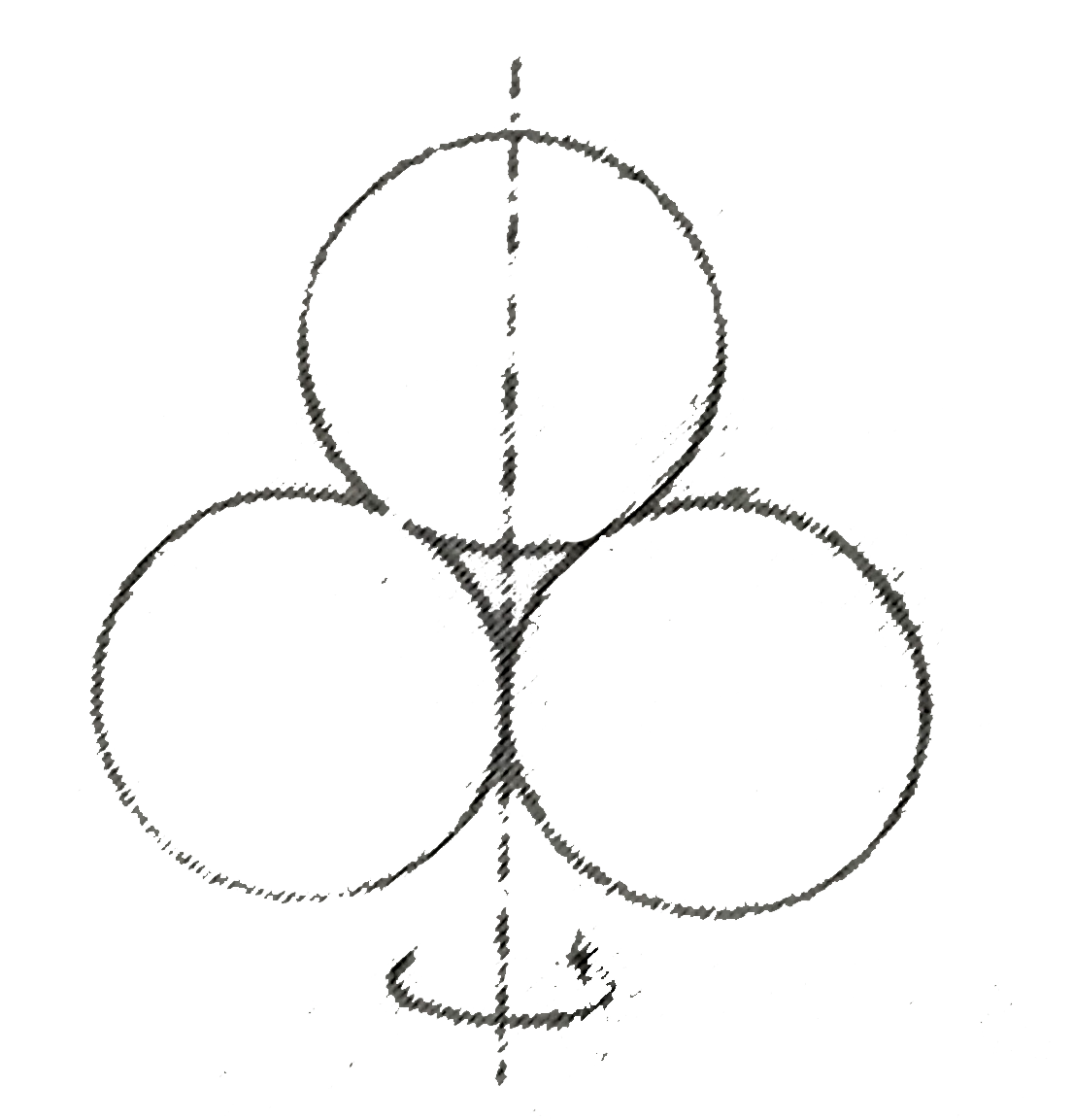A√65rB√56rC√67rD√76r - Question 3 - Select One
A ring of radius 1m is in xy-plane with centre at the origin. In each of option below, the moment of inertia of the ring about the line is calculated. In which case does the ring have same of inertia as that about z-axis.
Ay=γBx+y=1√2C−x−y=1√2Dx=1√2
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA thin circular ring of mass M and radius r is rotating about its ais with an angular speed ω. Two particles having mas m each are now attached at diametrically opposite points. The angular speed of the ring will become
View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View Solution