ABC is an equilateral triangle. Length of each side is 'a' and centroid is point O.Find
(i) −−→AB+−−→BC+−−→CA=?
(ii) −−→OA+−−→OB+−−→OC=?
(iii) If ∣∣∣−−→AB+−−→BC+−−→AC∣∣∣= na then n = ?
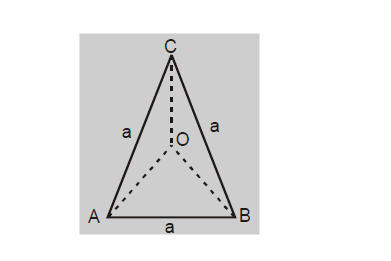
(iv) If −−→AB+−−→AC=n−−→AO then n = ?
Video Solution
Text Solution
(i) −−→AB,−−→BC&−−→CA form a closed triangle in the same order. Therefore their resultant is zero.
∴−−→AB+−−→BC+−−→CA=→0
(ii) −−→OA,−−→OBand−−→OC are three vectors of equal magnitude which are separated by equal angles of 120°. Therefore their resultant is zero.
∴−−→OA+−−→OA+−−→OC=→0
(iii) Here −−→AB+−−→BC=−−→AC
∴(−−→AB+−−→BC)+−−→AC=−−→AC+−−→AC=2−−→AC
∴∣∣∣−−→AB+−−→BC+−−→AC∣∣∣=∣∣∣2−−→AC∣∣∣=2∣∣∣−−→AC∣∣∣=2a
∴n=2
(iv) −−→AB+−−→AC=?
here −−→AB=−−→AO+−−→OB
and −−→AC=−−→AO+−−→OC
Adding the above two equations,
∴−−→AB+−−→AC=2−−→AO+−−→OB+−−→OC ......(1)
but −−→OA+−−→OB+−−→OC=→0
[from (ii) part of question]
∴−−→OB+−−→OC=−−−→OA=−−→AO ....(2)
using equations (1) and (2)
−−→AB+−−→AC=2−−→AO+−−→AO
−−→AB+−−→AC=3−−→AO n=3
|
Topper's Solved these Questions
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 1
36 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 2
33 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - PRACTICE QUESTION
4 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
15 Videos
Similar Questions
Knowledge Check
In a triangle ABC, if taken in order, consider the following statements:
1.−−→AB+−−→BC+−−→CA=→0
2. −−→AB+−−→BC−−−→CA=→0
3. −−→AB−−−→BC+−−→CA=→0
4. −−→BA−−−→BC+−−→CA=→0
How many of the above statements are correct?AOneBTwoCThreeDFourIn a triangle ABC, if taken in order, consider the following statements
1. −−→AB+−−→BC+−−→CA=→0
2 −−→AB+−−→BC−−−→CA=→0
3. −−→AB−−−→BC+−−→CA=→0
4. −−→BA−−−→BC+−−→CA=→0
How many of the above statements are correct?AoneBtwoCThreeDFourIf ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
In a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionIn the regular hexagon shown in figure −−→AB+−−→BC+−−→CD+−−→DE+−−→EF+−−→AF can be expressed as :
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View SolutionABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
View SolutionIn a right angled triangle hypotenuse AC= p, then −−→AB.−−→AC+−−→BC.−−→BA+−−→CA.−−→CB equal to ?
View Solution
