Vectors →A,→Band→C are shown in figure. Find angle between
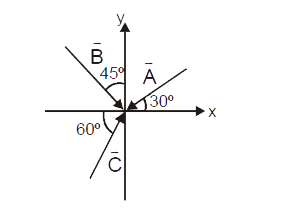
(i)→Aand→B (ii)→Aand→C (iii)→Band→C.
The correct Answer is:(i)105∘,(ii)150∘,(iii)105∘
Step by step video & image solution for Vectors vecA,vecB and vecC are shown in figure. Find angle between (i) vecA and vecB " " (ii) vecA and vecC" " (iii) vecB and vecC. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 2
33 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - PRACTICE QUESTION
4 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
15 Videos
Similar Questions
Three vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
View SolutionIf →A,→B,→C represents the three sides of an equilateral triangle taken in the same order then find the angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.

View Solution
Knowledge Check
Let →a,→b,→c be three unit vectors such that angle between →aand→bisα,→band→c is βand→cand→a is γ. if ∣∣→a.+→b+→c∣∣=2 , then cosα+cosβ+cosβ =
A1B−12C32D12→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
Aπ/2Bπ/4C3π/4Dπ
If |→a|+∣∣→b∣∣=|→c|and→a+→b=→c then find the angle between →aand→b.
View SolutionIf |→a|=∣∣→b∣∣=|→c|and→a+→b=→c then find the angle between →aand→b.
View SolutionLet →A,→Band→C be unit vectors such that →A.→B=→A.→C=0 and the angle between →Band→C beπ/3. Then →A=±2(→B×→C).
View SolutionConsider three vectors →A,→Band→C as shown in fig. perform graphically the following vector additions and subtractions (a) →A+→B
(b). →A+→B+→C
(c). →A−→B
(d). →A+→B−→C

View SolutionLet →A,→Band→C be vectors of legth , 3,4and 5 respectively. Let →A be perpendicular to →B+→C,→B to →C+→Aand→C to→A+→B then the length of vector →A+→B+→C is __________.
View SolutionLet →A,→Band→C be vectors of legth , 3,4and 5 respectively. Let →A be perpendicular to →B+→C,→B to →C+→Aand→C to→A+→B then the length of vector →A+→B+→C is __________.
View Solution
