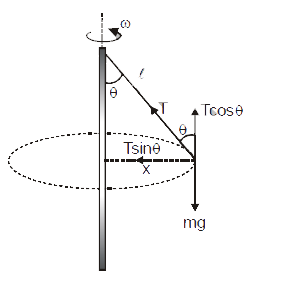
A vertical rod is rotating about its axis with a uniform angular speed ω . A simple pendulum of length l is attached to its upper end what is its inclination with the rod ?
Let the radius of the circle in which the bob is rotating is, the tension in the string is T, weight of the bob mg, and inclination of the string θ. Then T cos θ balances the weight mg and T sin θ provides the centripetal force necessary for circular motion.
That is -
T cos θ = mg
and T sin θ=mω2 x
but x = l sin θ
∴ T=mω2 l
and cos θ=mgT=mgmω2 l
or θ=cos−1(gω2l)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE -141videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 216videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II20videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - COMMUNICATION SYSTEMEXERCISE - EXERCISE - 36videos
COMMUNICATION SYSTEM
Similar Questions
(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod.View SolutionFind the angular momentum about the axis of rotation and kinetic energy.
(a) A uniform circular disc of mass m and radius R rotating about its diameter with an angular speed ω.
(b) A uniform square plate of mass m and edge L rotating about its diagonal with an angular speed ω.View Solution
Knowledge Check
- Question 1 - Select One
A pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
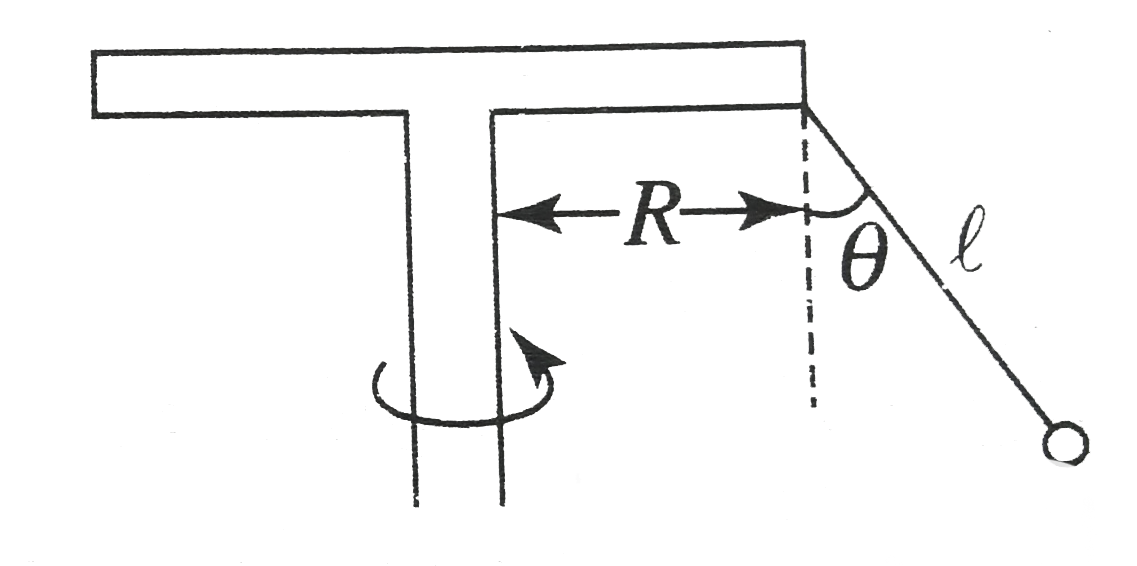 Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ
Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ - Question 2 - Select One
Two point masses A of mass M and B of mass of 4M are fixed at the ends of a rod of length l and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass A is at
A25lB85lC45lDl5 - Question 3 - Select One
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
L shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed ω .The sleeve has mass m and friction coefficient between rod and sleeve is μ.The minimum angular speed ω for which sleeve cannot slip on rod is?
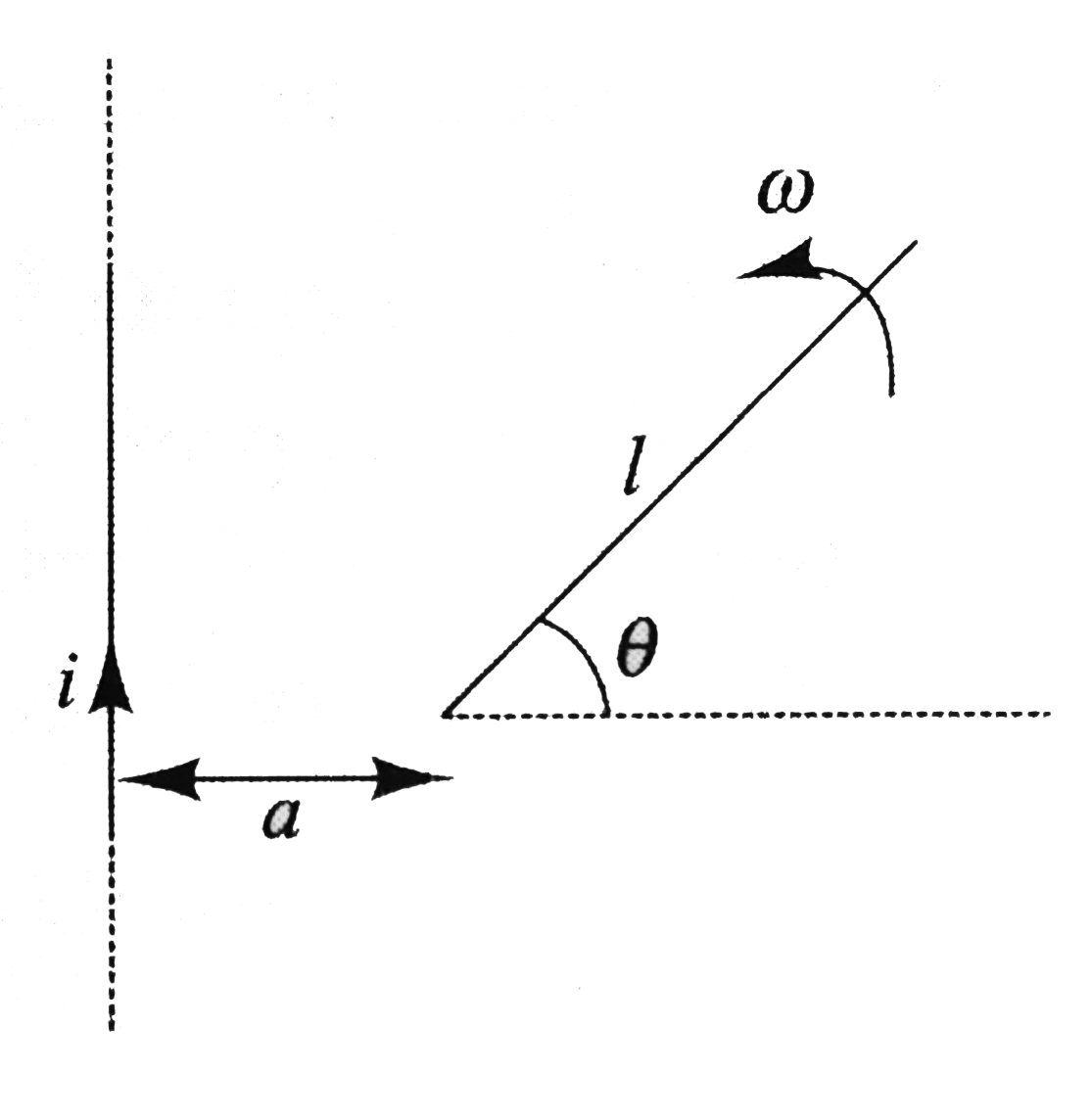
View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.
 View Solution
View SolutionA bicycle wheel (ring) of mass 1kg and radius 2m is attached at the end of a long rod of mass 1kg and length 3m, with the axis of wheel perpendicular to the rod. The rod is rotating counter clockwise as seen from above about its other end with an angular speed 0.5 rad/s. If wheel is also rotating about its axis with same angular speed in counter clock wise sense as seen from above. Find angular momentum of the system (in kg-m/s) about the axis passing through one end of rod. (Neglect mass of spokes and mass of rod connecting end of length 3m and centre of ring).
View SolutionA uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely lonf wire carrying current i. Find the emf induced in the rod at the instant shown in .
 View Solution
View Solution

