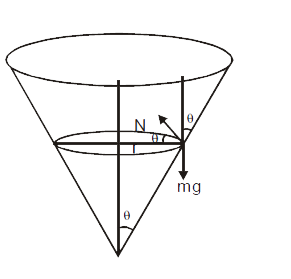
A particle describes a horizontal circle of radius r in a funnel type vessel of frictionless surface with half one angle θ (as shown in figure). If mass of the particle is m, then in dynamical equilibrium the speed of the particle must be -
The normal reaction N and weight mg are the only forces acting on the particle (inertial frame view),
the N is making an angle (π2−θ) with the vertical.
The vertical component of N balances the weight mg and the horizontal component provides the centripetal force required for circular motion. Thus
N cos (π2−θ) = mg
N sin (π2−θ)=mv2r
or N sin θ = mg.
N cos θ=mv2r,
on dividing we get tan θ=rgv2,
so v = √rgtanθ
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE -141videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 216videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II20videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - COMMUNICATION SYSTEMEXERCISE - EXERCISE - 36videos
COMMUNICATION SYSTEM
Similar Questions
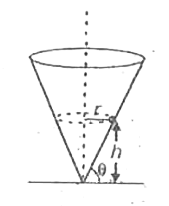
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
 View Solution
View SolutionA particle describing circular motion as shown in figure. The velocity of particle in m s is-
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a particle covers half the circle of radius R with constant speed then
AMomentum change is mvrBChange in K.E is 1/2mvCChange in K.E is mvDChange in K.E is zero - Question 2 - Select One or More
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulu) as shown in the figure. If speed of the particle is constant then,
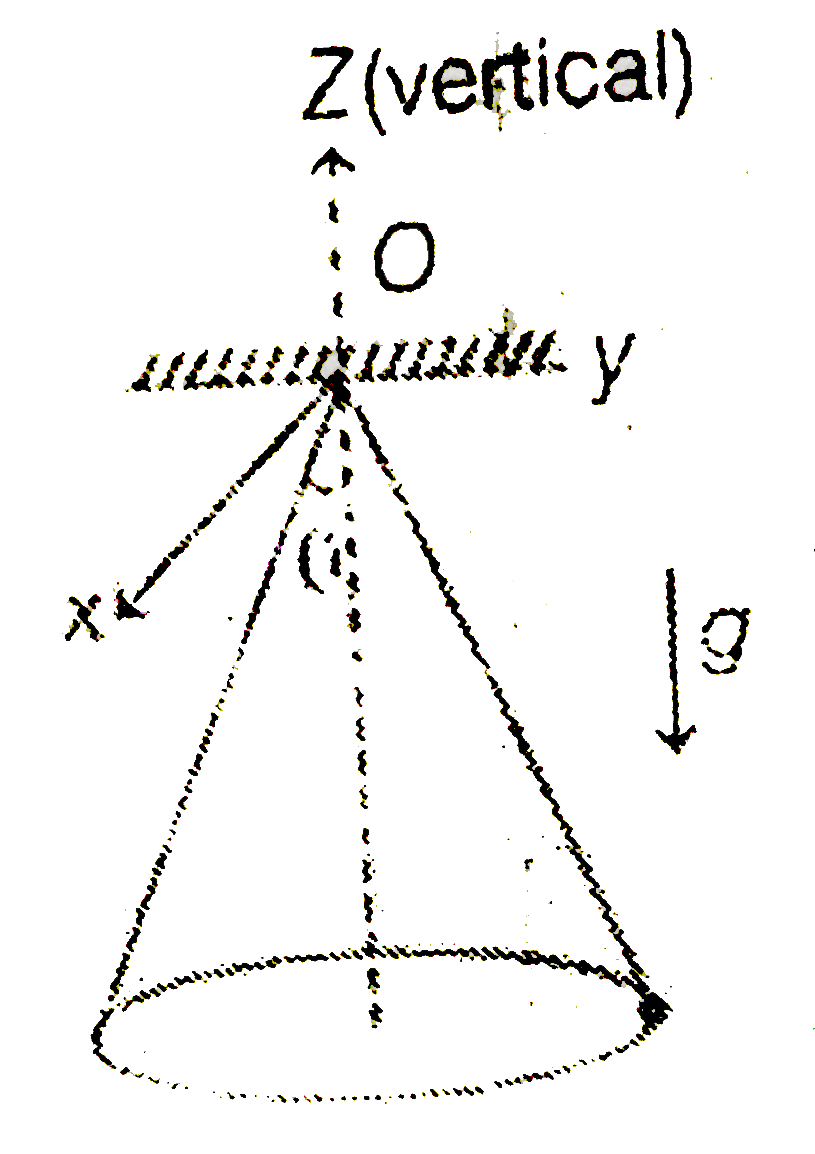 Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero.
Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero. - Question 3 - Select One
A particle moves with a speed v in a circle of radius R.The x-component of the average velocity of the particle in a half- revolution, as shown in figure−3.76,is:
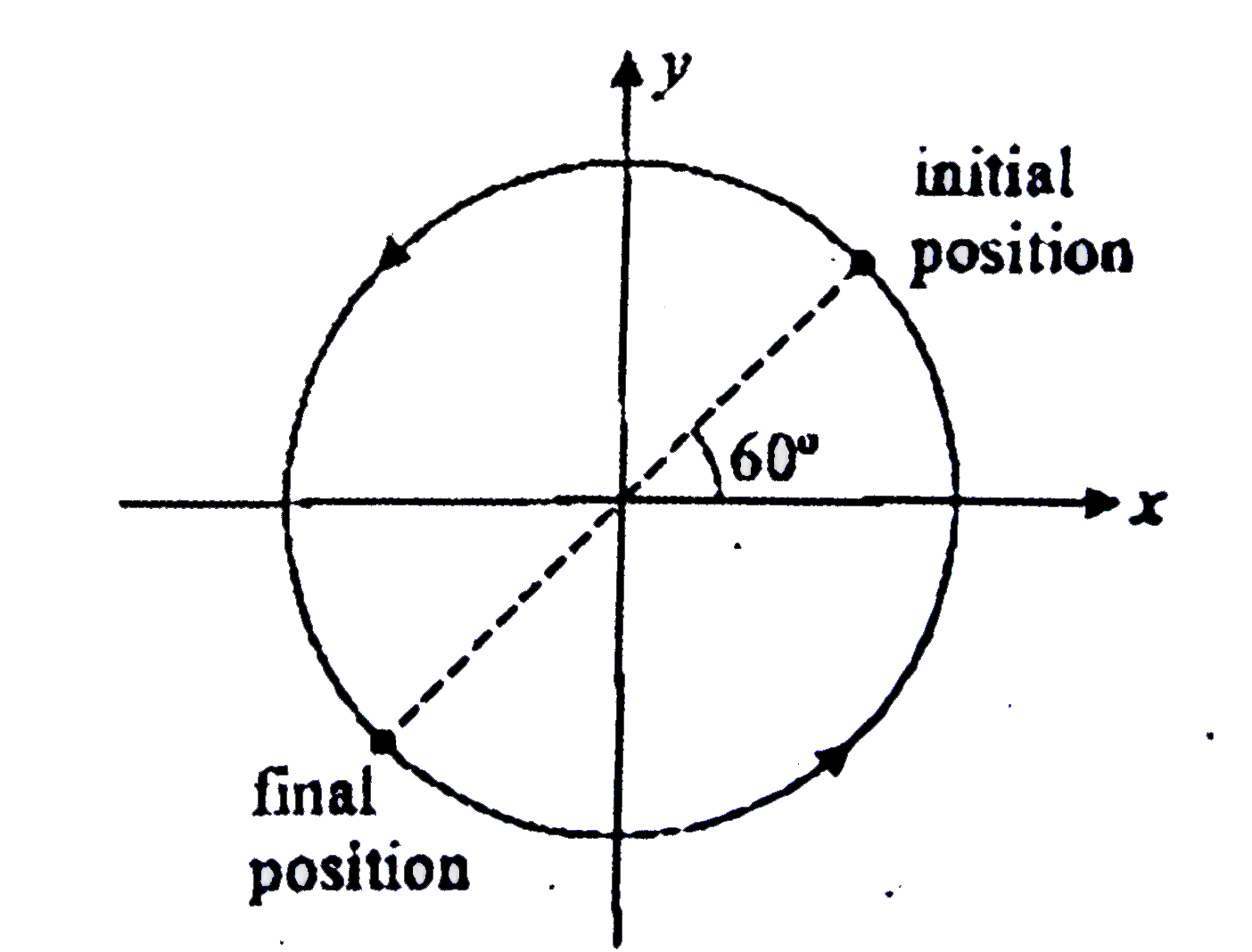 A−vπB−v2πC−v4πD−2vπ
A−vπB−v2πC−v4πD−2vπ
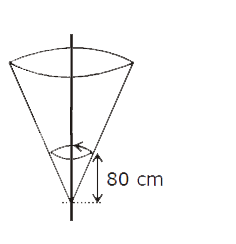
A particle describes a horizontal circle on the smooth inner surface of a conical funnel as shown in figure - 3.44. If the height of the plane of the circle above the vertex is 9.8 cm, find the speed of the particle.
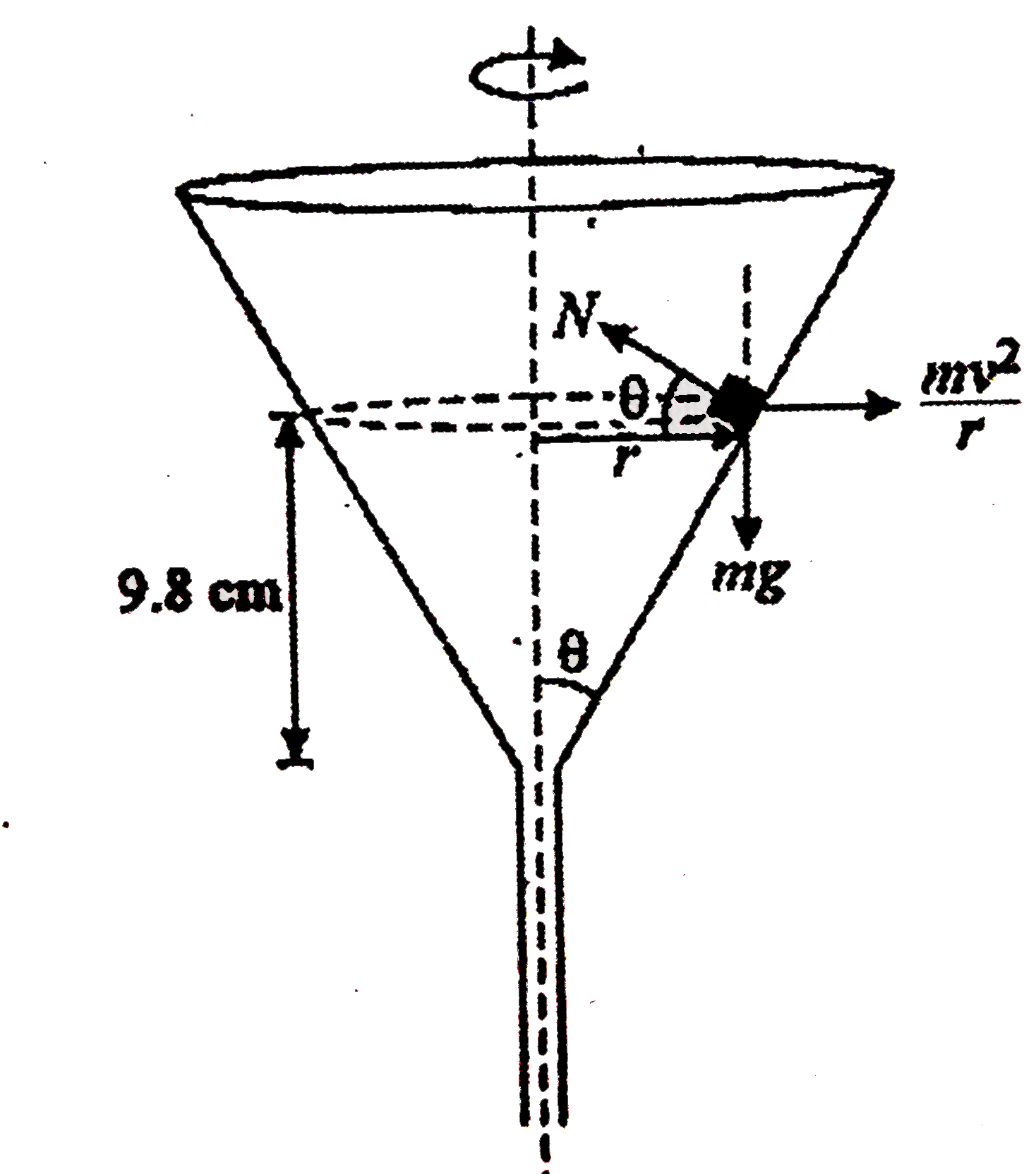 View Solution
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
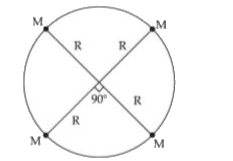 View Solution
View SolutionA particle describes a horizontal circule on the smooth inner surface of a coincal funnel as shown in Fig. If the height of the plane of the circle above the vertex is 9.8cm, find the speed of the particle.
View SolutionA particle describes a horizontal circle on smooth inner surface of a conical funnel as shown. If the height of the plane of the circle. Above the vertax is 10cm, find the speed of the paricle.
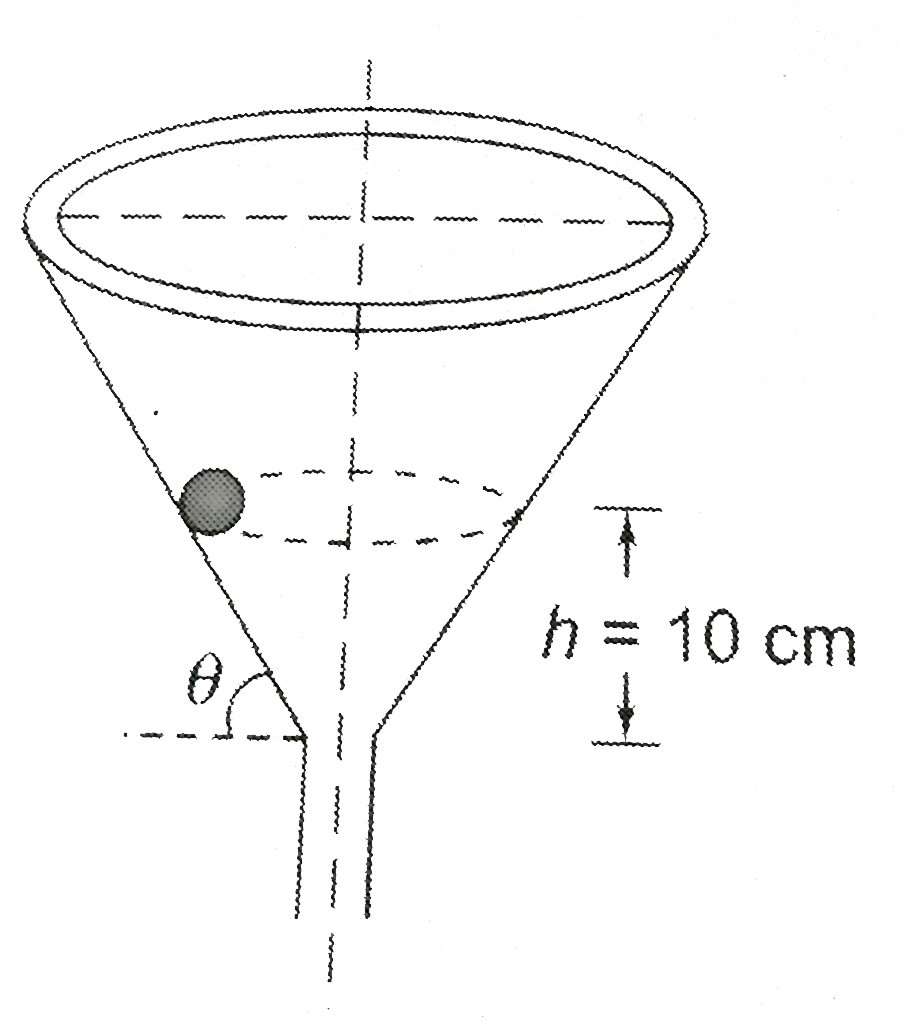 View Solution
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View Solution
