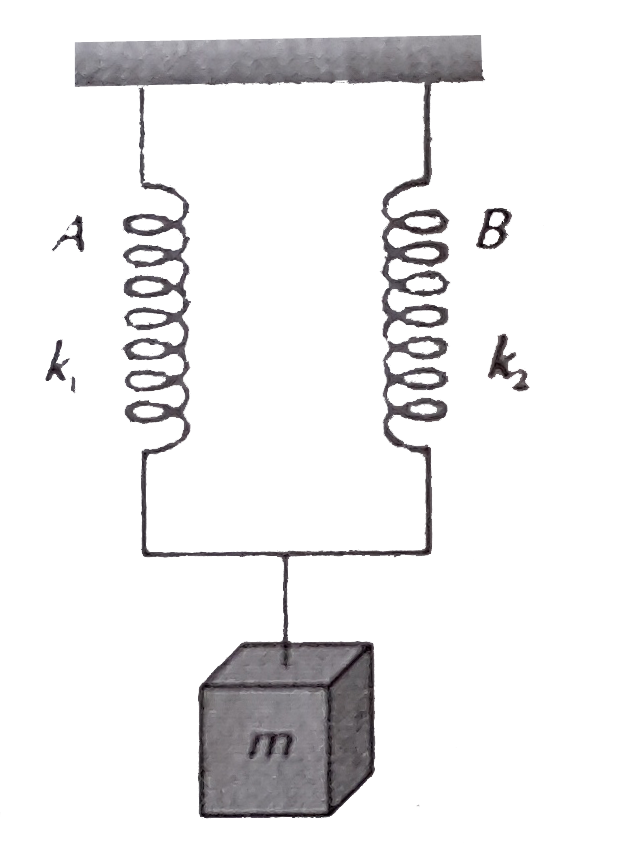
The spring constants of two springs of same length are k1 and k2 as shown in figure. If an object of mass m is suspended and set in vibration , the period will be
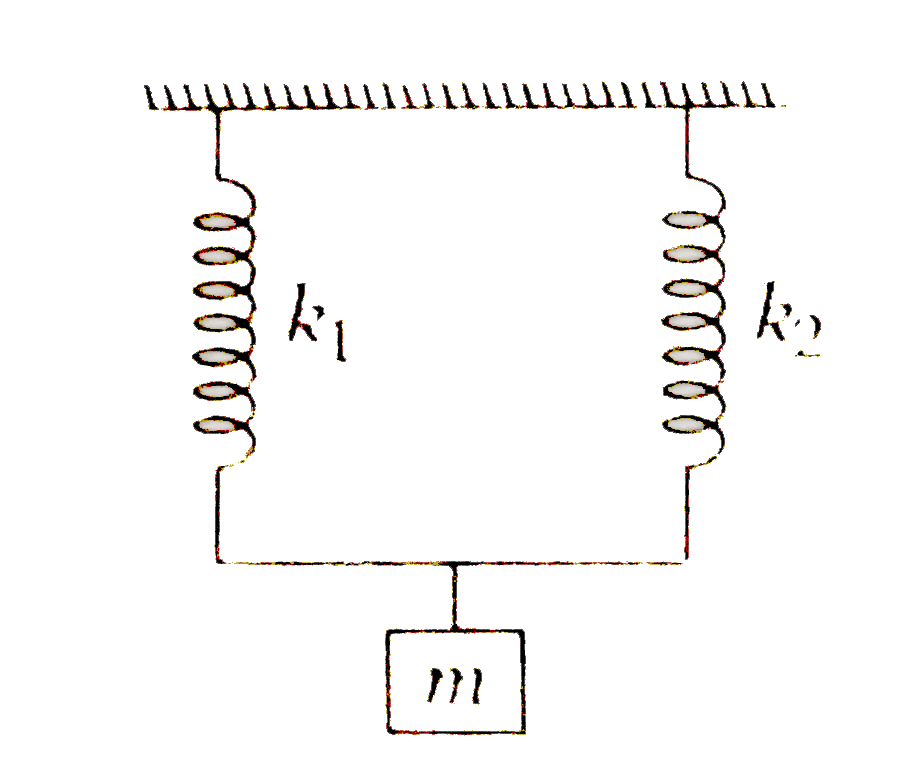
2π√mk−1k2
2π√mk1k2
2π√mk1−k2
2π√/(k1+k2)
The correct Answer is:D
Step by step video & image solution for The spring constants of two springs of same length are k_(1) and k_(2) as shown in figure. If an object of mass m is suspended and set in vibration , the period will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum
6 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]
11 Videos
Similar Questions
Two identical spring of constant K are connected in series and parallel as shown in figure. A mass mis suspended from them. The ratio of their frequencies of vertical oscillations will be
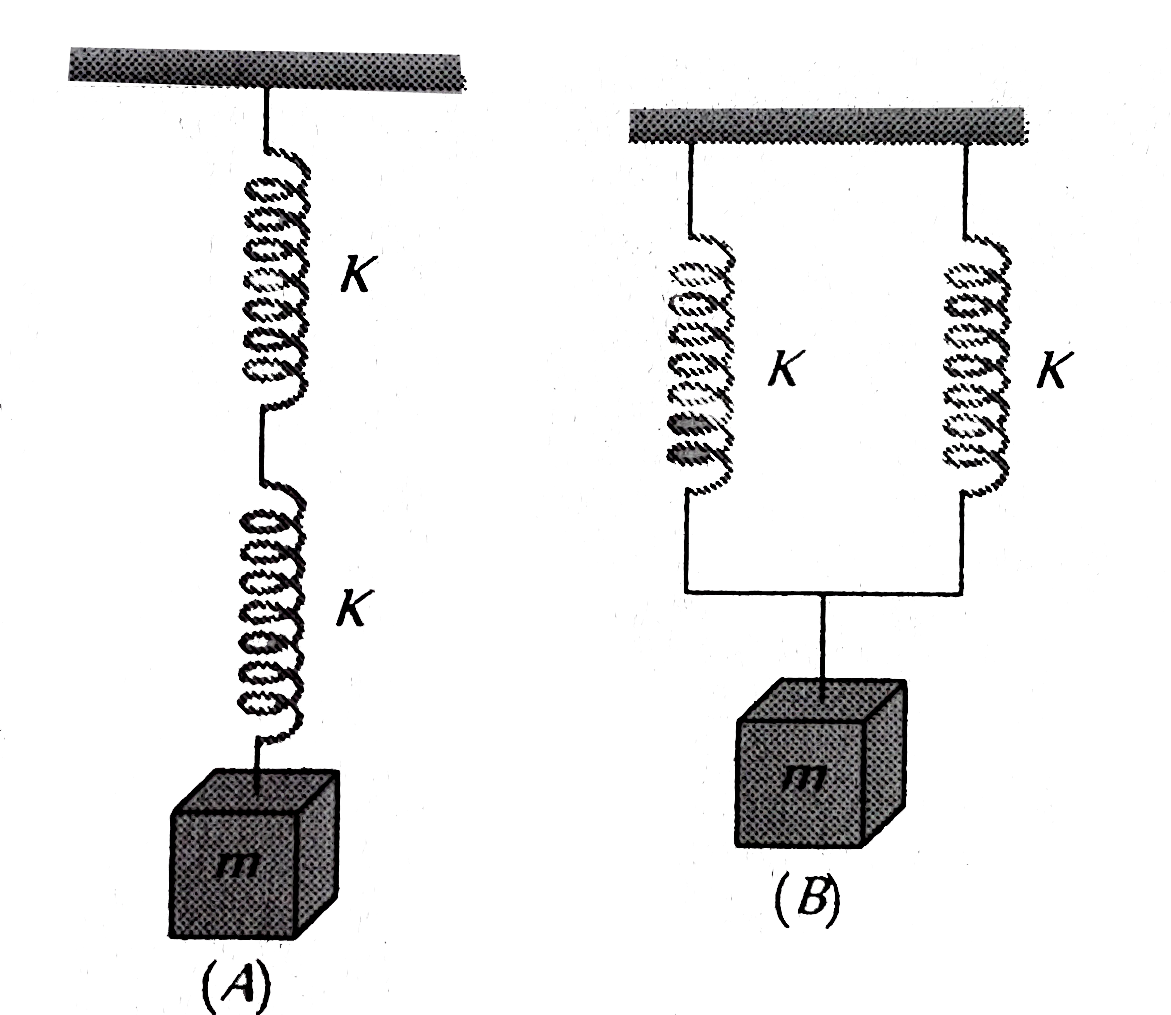
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
Two identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
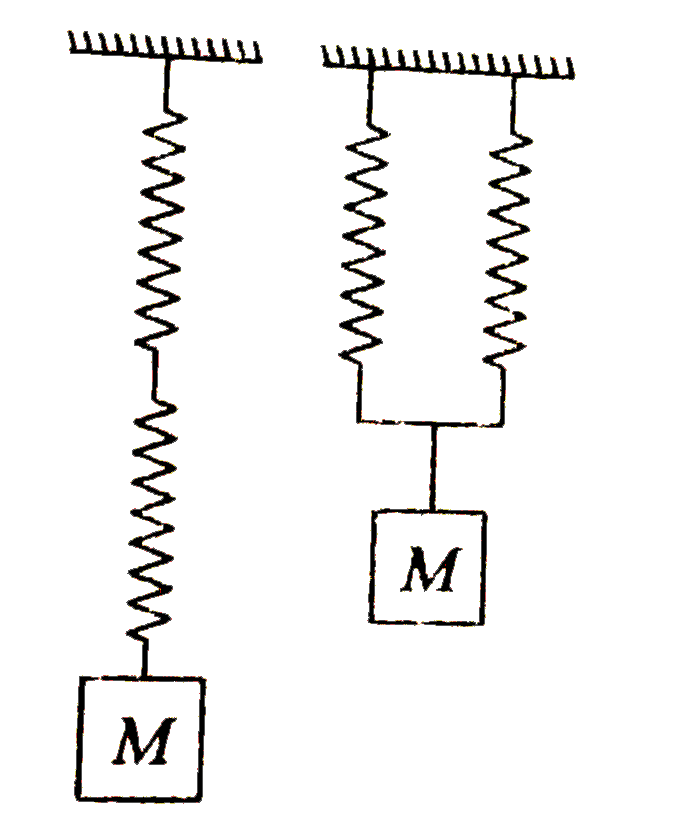 A1:2B2:1C4:1D1:4
A1:2B2:1C4:1D1:4A spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
A2π√2m9KB2π√m9KC2π√2m5KD2π√m5KTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
A block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
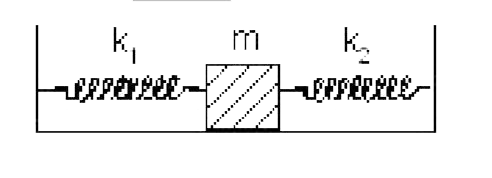
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionA system consists of two spring and a mass m = 1 kg as shown in figure . If mass m is dispalced slightly along vertical and vertical and released. The system oscillates with a period of 2 s .Then , the spring canstant K is

View SolutionA mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be

View SolutionA mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be
View Solution
