In the compound pendulum, the minimum period of oscillation will be :
2π√kg
2π√lg
2π√2lg
2π√2kg
The correct Answer is:D
To find the minimum period of oscillation for a compound pendulum, we can follow these steps:
1. Understand the Formula for the Time Period:
The time period T of a compound pendulum is given by the formula:
T=2π√Iomgd
where Io is the moment of inertia about the point of suspension, m is the mass, g is the acceleration due to gravity, and d is the distance from the point of suspension to the center of mass.
2. Apply the Parallel Axis Theorem:
According to the parallel axis theorem, the moment of inertia Io can be expressed as:
Io=Icg+md2
where Icg is the moment of inertia about the center of mass.
3. Substitute Io into the Time Period Formula:
Substituting Io into the time period formula gives:
T=2π√Icg+md2mgd
4. Replace Icg with mk2:
Here, k is the radius of gyration, so we can write:
Icg=mk2
Thus, the time period becomes:
T=2π√mk2+md2mgd=2π√k2+d2gd
5. Minimize the Time Period:
To find the minimum period, we need to minimize the expression:
f(d)=k2+d2d
This can be rewritten as:
f(d)=k2d+d
6. Differentiate and Set to Zero:
Differentiate f(d) with respect to d:
f′(d)=−k2d2+1
Setting f′(d)=0 gives:
−k2d2+1=0⟹k2d2=1⟹d2=k2⟹d=k
7. Substitute Back to Find Minimum Time Period:
Substitute d=k back into the time period formula:
T=2π√k2+k2gk=2π√2k2gk=2π√2kg
Final Result:
The minimum period of oscillation for the compound pendulum is:
T=2π√2kg
The time period T of a compound pendulum is given by the formula:
T=2π√Iomgd
where Io is the moment of inertia about the point of suspension, m is the mass, g is the acceleration due to gravity, and d is the distance from the point of suspension to the center of mass.
According to the parallel axis theorem, the moment of inertia Io can be expressed as:
Io=Icg+md2
where Icg is the moment of inertia about the center of mass.
Substituting Io into the time period formula gives:
T=2π√Icg+md2mgd
Here, k is the radius of gyration, so we can write:
Icg=mk2
Thus, the time period becomes:
T=2π√mk2+md2mgd=2π√k2+d2gd
To find the minimum period, we need to minimize the expression:
f(d)=k2+d2d
This can be rewritten as:
f(d)=k2d+d
Differentiate f(d) with respect to d:
f′(d)=−k2d2+1
Setting f′(d)=0 gives:
−k2d2+1=0⟹k2d2=1⟹d2=k2⟹d=k
Substitute d=k back into the time period formula:
T=2π√k2+k2gk=2π√2k2gk=2π√2kg
The minimum period of oscillation for the compound pendulum is:
T=2π√2kg
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET24videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum6videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]11videos
SIMPLE HARONIC MOTION
Similar Questions
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum . How does it differ fro the time period calculated using the formula for a simple pendulum?
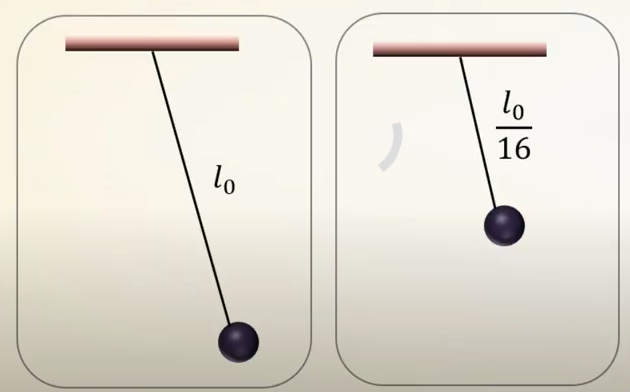
View SolutionA simple pendulum of length l0 can perform simple harmonic oscillations with a time period T0. If the length of the pendulum is decreased to l016 then the time time period of oscillation will become.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For a compound pendulum, the maximum time period is :
A2π√LgB2π√2kgCZeroDInfinite - Question 2 - Select One
The time period of a simple pendulum in air is T. Now the pendulum is submerged in a liquid of density ρ16 where ρ is density of the bob of the pendulum. The new time period of oscillation is.
A4√15TB√415TC√154TD√153T - Question 3 - Select One
In a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
AL/T=ConstantBL2/T2= ConstantCL/T2=ConstantDLT=Constant
A compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
View SolutionA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
View SolutionThe time period of oscillations of a simple pendulum is 1 minute. If its length is increased b 44% then its new time period of oscillation will be
View SolutionA seconds pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket
View SolutionConsider a simple pendulum. The period of oscillation of the simple pendulum depends on its length and acceleration due to gravity. Then the expression for its time period is
View Solution

