Water rises in a capillary upto a height of 4 cm. If it is tilted to 30∘ from the vertical, then the length of water column in it will be-
8√3cm
8√3cm
4 cm
2 cm
The correct Answer is:A
To solve the problem of how the height of water in a capillary tube changes when the tube is tilted at an angle of 30 degrees, we can follow these steps:
Step 1: Understand the initial conditions
The water rises to a height h1=4cm when the capillary tube is vertical. This height is determined by the balance of forces acting on the water column due to surface tension and gravity.
Step 2: Identify the formula for capillary rise
The formula for the height of liquid rise in a capillary tube is given by:
h=2Tcosθρgr
where:
- T = surface tension of the liquid,
- θ = angle of contact (for vertical, θ=0 and cos(0)=1),
- ρ = density of the liquid,
- g = acceleration due to gravity,
- r = radius of the capillary tube.
Step 3: Analyze the situation when the capillary is tilted
When the capillary tube is tilted at an angle θ=30∘, the effective gravitational force acting on the liquid changes. The vertical component of gravity acting on the liquid column is now gcos(30∘).
Step 4: Write the new height formula for the tilted capillary
The new height h2 when the capillary is tilted can be expressed as:
h2=2Tcos(30∘)ρgr
Step 5: Relate the heights h1 and h2
From the original height h1 when vertical, we have:
h1=2Tρgr
Now, we can find the ratio of the two heights:
h1h2=gcos(30∘)g
This simplifies to:
h1h2=cos(30∘)=√32
Step 6: Solve for h2
Rearranging gives us:
h2=2h1√3
Substituting h1=4cm:
h2=2×4√3=8√3cm
Final Answer
Thus, the length of the water column in the tilted capillary tube is:
h2=8√3cm
---
The water rises to a height h1=4cm when the capillary tube is vertical. This height is determined by the balance of forces acting on the water column due to surface tension and gravity.
The formula for the height of liquid rise in a capillary tube is given by:
h=2Tcosθρgr
where:
- T = surface tension of the liquid,
- θ = angle of contact (for vertical, θ=0 and cos(0)=1),
- ρ = density of the liquid,
- g = acceleration due to gravity,
- r = radius of the capillary tube.
When the capillary tube is tilted at an angle θ=30∘, the effective gravitational force acting on the liquid changes. The vertical component of gravity acting on the liquid column is now gcos(30∘).
The new height h2 when the capillary is tilted can be expressed as:
h2=2Tcos(30∘)ρgr
From the original height h1 when vertical, we have:
h1=2Tρgr
Now, we can find the ratio of the two heights:
h1h2=gcos(30∘)g
This simplifies to:
h1h2=cos(30∘)=√32
Rearranging gives us:
h2=2h1√3
Substituting h1=4cm:
h2=2×4√3=8√3cm
Thus, the length of the water column in the tilted capillary tube is:
h2=8√3cm
Topper's Solved these Questions
- SURFACE TENSIONBook:MOTIONChapter:SURFACE TENSIONExercise:Exercise - 2 Objective Problems | NEET
Explore 28 Videos
- SURFACE TENSIONBook:MOTIONChapter:SURFACE TENSIONExercise:Exercise - 3 | Section- A Previous Year Problems | NEET/Other
Explore 53 Videos
- SURFACE TENSIONBook:MOTIONChapter:SURFACE TENSIONExercise:SOLVED EXAMPLE
Explore 7 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
- SURFACE TENSION & VISCOSITY Book:MOTIONChapter:SURFACE TENSION & VISCOSITY Exercise:Exercise - 4 | Level-II Previous Year | JEE Advanced
Explore 12 Videos
Similar Questions
Water rises in a capillary upto a height of 8.0 cm. if the capillary is inclined at an angle of 45∘ with the vertical then determine the vertical height of water. How much length of the capillary will be occupied by water ? If the length of the capillary is reduced to 4.0 cm and it is held vertically in water then what will be the position of water?
View SolutionWater rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45∘, the length of water risen in the tube will be
View Solution
Knowledge Check
Water rises in a capillary upto a height h. If now this capillary is tilted by an angle of 45∘ then the length of the water column in the capillary becomes-
A2hBh2Ch√2Dh√2Water rises in a capillary tube to a height h. It will rise to a height more than h
Aon the surface of sunBin a lift moving down with an accelerationCat the polesDin a lift moving up with an accelerationWater rises in a vertical capillary tube up to a height of 2.0 cm. If the tube is inclined at an angle of 60∘ with the vertical, then up to what length the water will rise in the tube ?
A2.0 cmB4. 0 cmC6. 0 cmD8. 0 cm
water rises in a capillary tube to a height of 1 cm. In another capillary where the radius is one-third of it, how high will the water rise (in cm)?
View SolutionWater rises in a capillary tube to a height H, when the capillary tube is vertical. If the same capillary is now inclined to the vertical the length of water column in it will
View SolutionWater rises to a height of 5 cm when a narrow glass tube is dipped vertically in it . If the tube is inclined at 60∘ to the vertical , then the rise of water in the capillary tube will be
View SolutionWater rises to a height of 2cm in a capillary tube. If the tube is tilted 60∘ from the vertical, water will rise in the tube to a length of
View Solution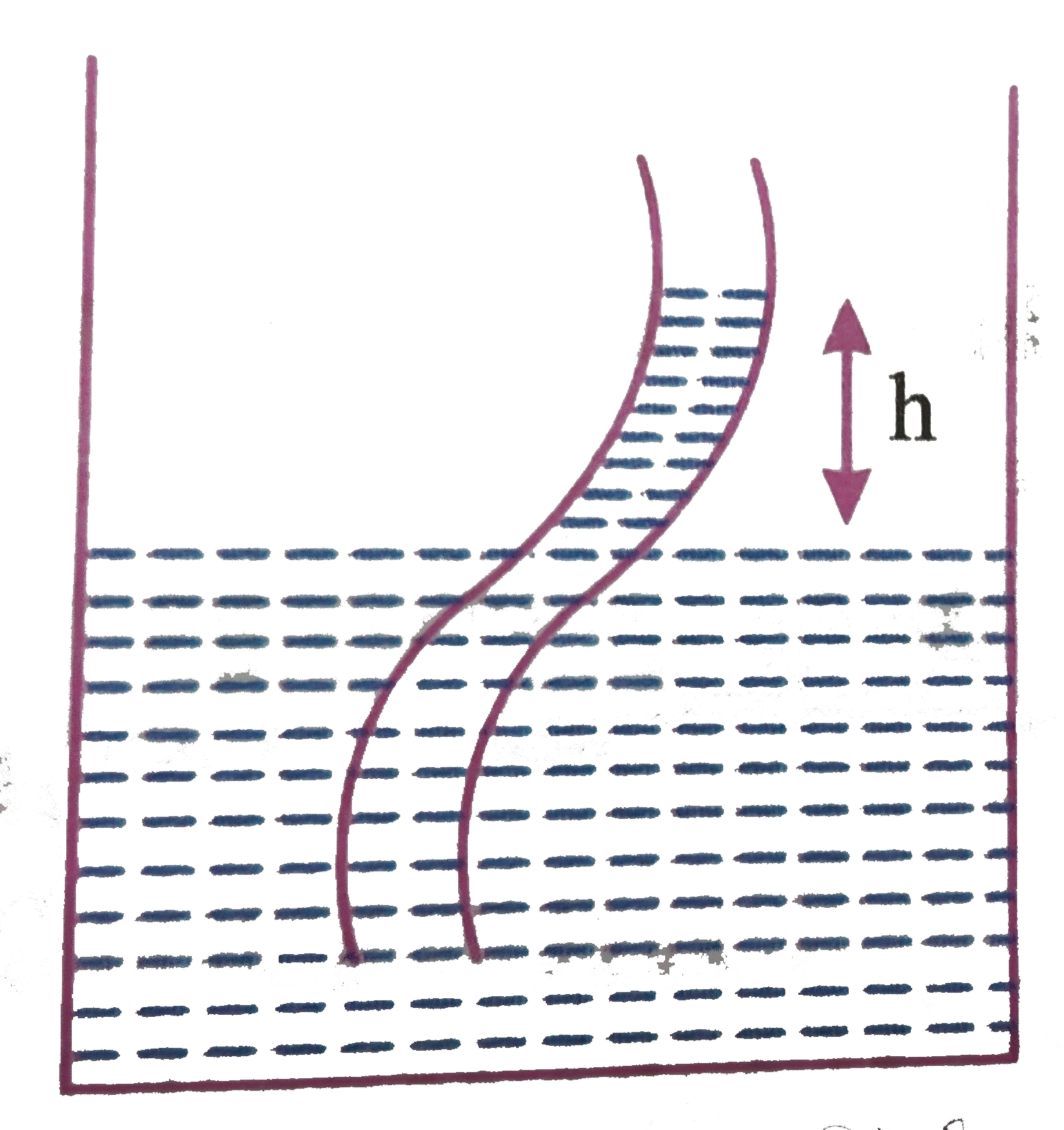
Water rises in a straight capillary tube upto a height of 5 cm when held vertical in water. If the tube is bent as shown figure then the height of water column in it will be
View Solution
