If |A|>19, which of the following could not be equal to A?
26
22
18
−20
The correct Answer is:C
To solve the problem, we need to determine which of the given options cannot be equal to A given that |A|>19.
1. Understanding the Absolute Value Condition:
We know that the absolute value |A| is defined as:
- |A|=A if A≥0
- |A|=−A if A<0
Given |A|>19, this means that A can either be greater than 19 or less than -19.
2. Evaluating Each Option:
Let's evaluate each option one by one to see if they satisfy the condition |A|>19.
- Option 1: A=26
Since A=26 is greater than 0, we have:
|A|=26
Since 26>19, this option is valid.
- Option 2: A=22
Again, since A=22 is greater than 0, we have:
|A|=22
Since 22>19, this option is also valid.
- Option 3: A=18
Here, since A=18 is also greater than 0, we have:
|A|=18
Since 18 is not greater than 19, this option cannot satisfy the condition |A|>19.
- Option 4: A=−20
Since A=−20 is less than 0, we have:
|A|=−(−20)=20
Since 20>19, this option is valid.
3. Conclusion:
The only option that does not satisfy the condition |A|>19 is Option 3: A=18.
Final Answer:
The option that could not be equal to A is Option 3: A=18.
---
We know that the absolute value |A| is defined as:
- |A|=A if A≥0
- |A|=−A if A<0
Given |A|>19, this means that A can either be greater than 19 or less than -19.
Let's evaluate each option one by one to see if they satisfy the condition |A|>19.
Since A=26 is greater than 0, we have:
|A|=26
Since 26>19, this option is valid.
Again, since A=22 is greater than 0, we have:
|A|=22
Since 22>19, this option is also valid.
Here, since A=18 is also greater than 0, we have:
|A|=18
Since 18 is not greater than 19, this option cannot satisfy the condition |A|>19.
Since A=−20 is less than 0, we have:
|A|=−(−20)=20
Since 20>19, this option is valid.
The only option that does not satisfy the condition |A|>19 is Option 3: A=18.
The option that could not be equal to A is Option 3: A=18.
Similar Questions
Knowledge Check
- Question 1 - Select One
If |A|>19, which of the following cannot be equal to A?
A26B22C18D−20 - Question 2 - Select One
Which of the following could be an integer?
AThe average of two consecutive integersBThe average of three consective integersCThe average of four consecutive integersDThe average of six consecutive integers - Question 3 - Select One
When x is divided by 3 remainder is z.In terms of z, which of the following could be equal to x?
Az−3B3−zC3zD6+z
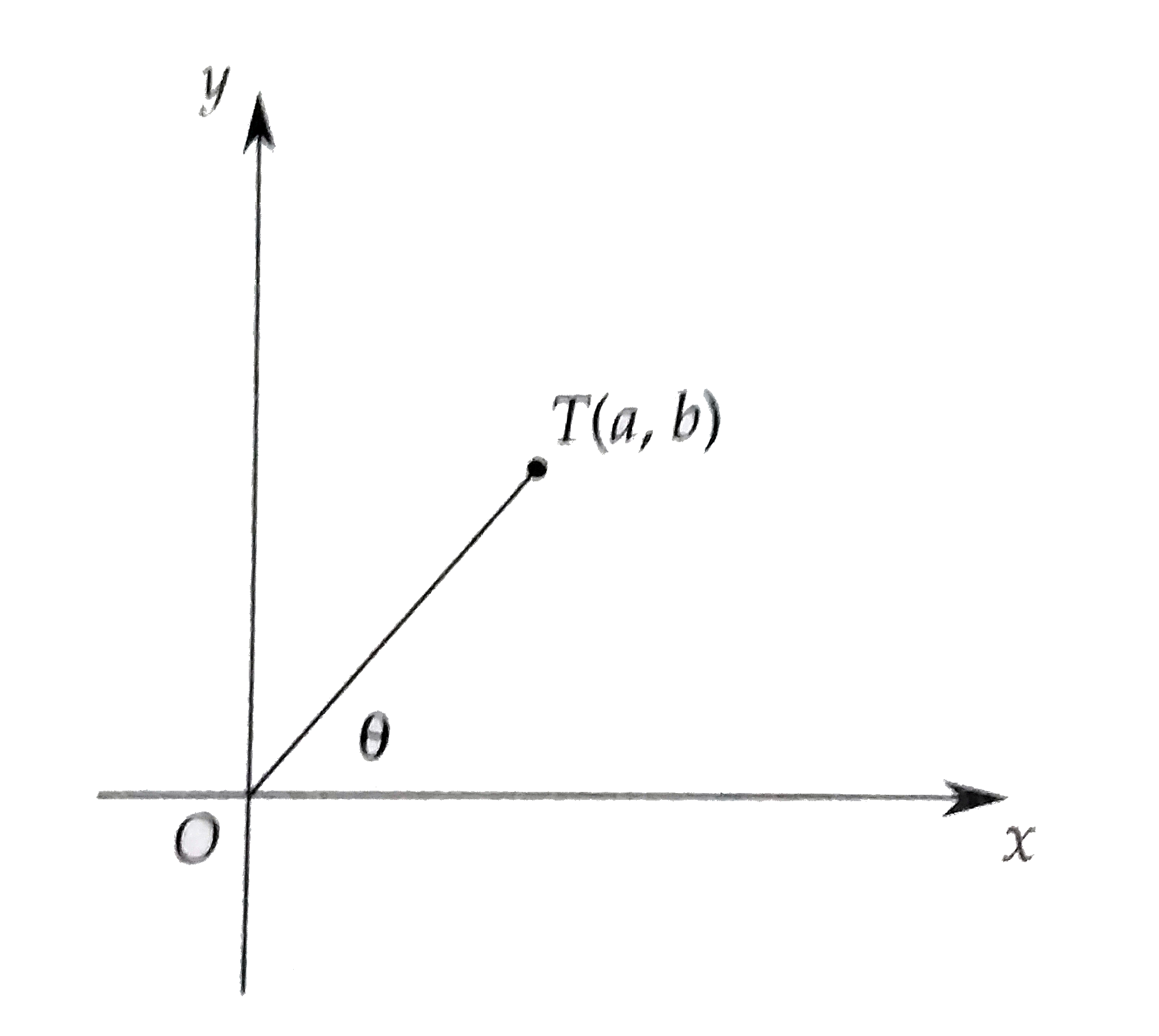
Which of the following is equal to cosθ ?
 View Solution
View SolutionIf G2<G, which of the following could be G ?
View SolutionIf x2−y2=16andx+y>x−y, then which one of the following could x−y equal ?
View Solution
In the figure above l2∣∣l3, which of the following could be false?View SolutionWhich of the following could be the graph of y=3−2x ?
View Solution

