ABCD is a parallelogram and APQ is a straight line meeting BC at Pand DC produced at Q. prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.
Step by step video & image solution for ABCD is a parallelogram and APQ is a straight line meeting BC at Pand DC produced at Q. prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
ABCD is a parallelogram and APQ is a straight line meeting BC at PandDC produced at Q. prove that the rectangle obtained by BPandDQ is equal to the rectangle contained by ABandBC.
View SolutionABCD is a parallelogram and APQ is a straight line meeting BC at PandDC produced at Q. prove that the rectangle obtained by BPandDQ is equal to the rectangle contained by ABandBC.
View Solution
Knowledge Check
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2ABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
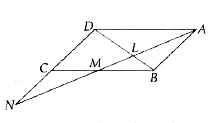
Given that DL =3LB , find ABCN .A3/2B1/2C4/5D1/4
ABCD is a parallelogram. Any line through A cuts DC at a point P and BC produced at Q.Then,
View SolutionABCD is a parallelogram; any line through A cuts DC at a point P and BC produced at Q. prove that triangle BCP is equal in area to triangle DPQ.
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.
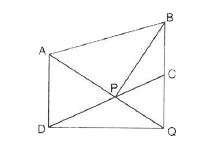
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.

View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View Solution
