चित्र 11.11 में 200 सेमी लम्बी एक नली में 0.90×103 किग्रा/ मी3 घनत्व का द्रव भरकर नली को ऊर्ध्वाधर से इतना झुका कर रखा गया है कि द्रव का तल A, निम्नतम बिंदु C से 100 सेमी ऊर्ध्वाधर दूरी पर है | नली में बिंदु A से 60 सेमी ऊर्ध्वाधर नीचे एक बिंदु B है | (a) यदि वायुमण्डलीय दाब 1.013×105 न्यूटन/मी2 हो, तो बिंदु A, B तथा C पर दाब ज्ञात कीजिए | (b) नली को सीधा रखने पर बिंदु C पर दाब कितना होगा ?
बिंदु A पर दाब = वायुमण्डलीय दाब P
=1.013×103 न्यूटन/मीटर2 |
बिंदु B पर दाब = वायुमण्डलीय दाब + द्रव की 60 सेमी (= 0.6 मीटर) ऊँचाई का दाब
=P+hdg
=(1.013×105)+[0.6×(0.9×103)×9.8]
=1.013×105+0.053×105
=1.066×105 न्यूटन/मीटर2 |
बिंदु C पर दाब = वायुमण्डलीय दाब +100 सेमी (= 1 मीटर) ऊँचे द्रव का दाब
=(1.013×105)+[1×(0.9×103)×9.8]
=1.013×105+0.0882×105
=1.101×105 न्यूटन/मीटर2 |
(b ) नली को सीधा करने पर बिंदु C पर दाब
= वायुमण्डलीय दाब + 200 सेमी (= 2 मीटर) ऊँचे द्रव स्तम्भ का दाब
=(1.013×105)+[2×(0.9×103)×9.8]
=1.013×105+0.1764×105
=1.189×105 न्यूटन/मीटर2 |
Topper's Solved these Questions
- तरल के यान्त्रिक गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - तथ्यात्मक प्रश्न
22 Videos
- तरल के यान्त्रिक गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - प्रश्न (वस्तुनिष्ठ प्रश्न )
10 Videos
- तरंगे BOOK - SHIVLAAL PUBLICATIONCHAPTER - तरंगे EXERCISE - वस्तुनिष्ठ प्रश्न
202 Videos
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - वस्तुनिष्ठ प्रश्न
79 Videos
Similar Questions
एक बीकर में किसी ऊँचाई तक द्रव भरा है | यदि द्रव की सतह पर लकड़ी का एक गुटका तैरा दिया जाए तो बीकर की तली पर पड़ने वाले दाब में क्या अंतर आएगा तथा क्यों ?
View Solutionकिसी द्रव में गहराई h पर कुल दाब होता है :
View Solution20 मीटर लम्बाई की एकसमान डोरी को एक दृढ़ आधार से लटकाया गया है। इसके निचले सिरों पर एक तरंग स्पन्द प्रवेश करती है। इसे ऊपर आधार तक पहुँचने में लगा समय होगा(g=10 मी/से2) :
View Solutionसरल आवर्त गति करते हुए एक कण के सम्बन्ध में असत्य कथन है :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solution△ABC में मध्यिकाएँ AD , BE और CF बिंदु G से गुजरती है।
यदि GF=4 सेमी हो तो GC का मान ज्ञात कीजिए।
View Solution△ABC में मध्यिकाएँ AD , BE और CF बिंदु G से गुजरती है।
यदि AD=7.5 सेमी हो तो GD का मान ज्ञात कीजिए।
View Solutionएक △ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AG=6 सेमी , BE=12.6 सेमी और FG=3 सेमी हो , तो AD ,GE और GC ज्ञात कीजिए।
View Solutionएक △ABC की मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AG=5 सेमी ,BE=12 सेमी और FG=3 सेमी हो तो AD ,GE और GC ज्ञात कीजिए।
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
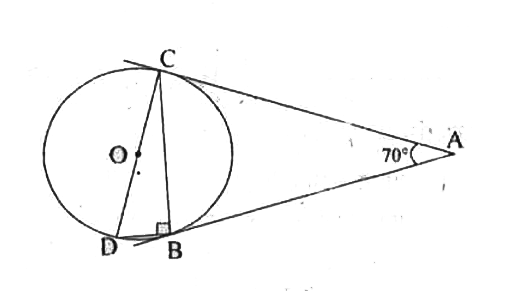
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solution
