A car of mass m travelling at speed v moves on a horizontal track so that the centre of mass describes a circle of radius r . Show that the limiting speed beyond which the car will overturn is given by
v2=grah
where 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground .
We consider the rear view of the car , centripetal force mv2r to the left is provided by frictional force acting on the tyres. From the force diagram ,

Sum of forces in vertical direction ,
R1+R2=mg...........(i)
Sum of forces in horizontal direction ,
F1+F2=mv2r ........ (ii)
Taking moments about the centre of mass G ,
(F1+F2)h+R1a=R2a
∴ F1+F2=(R2−R1)ah ......(iii)
Combining this with Eqn. (ii) to eliminate F1+F2 gives
R2−R1=hmv2ar ......(iv)
We now have two simultaneous Eqns.(i) and (iv) , for R1 and R2 . Solving these by adding and subtracting , we find that 2R1=mg−hmv2ar and 2R2=mg+hmv2ar
From these expressions it is clear that the inner wheels will leave the ground when R1 will become zero and the car begins to overturn , i .e., mg=hmv2ar
So , the limiting speed is given by v2=grah as required
Alternative solution : We choose the frame of refernce attached to the car , i.e., a fictitious centrifugal force of magnitude mv2/r , acts through the centre of mass G and directed away from the centre of the circle . At the instant when the car begins to overturn , the force R1 and F1 are zero , so the only forces acting on the car are R2,F2 the centrifugal force and the weight mg .
If the resultant P of the centrifugal force and the weight passes outside the point of contact with the ground (the outer wheels) as shown in Fig . 7.66 (b) , the couple on the car will be clockwise , causing it to overturn . The critical condition , when overturning is just about to occur , happens when the resultant P passes through the contact point . By using similar triangles , we can see that the condition for overturning is thus
mv2r+mg>ah
which gives v2>grah as before .
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
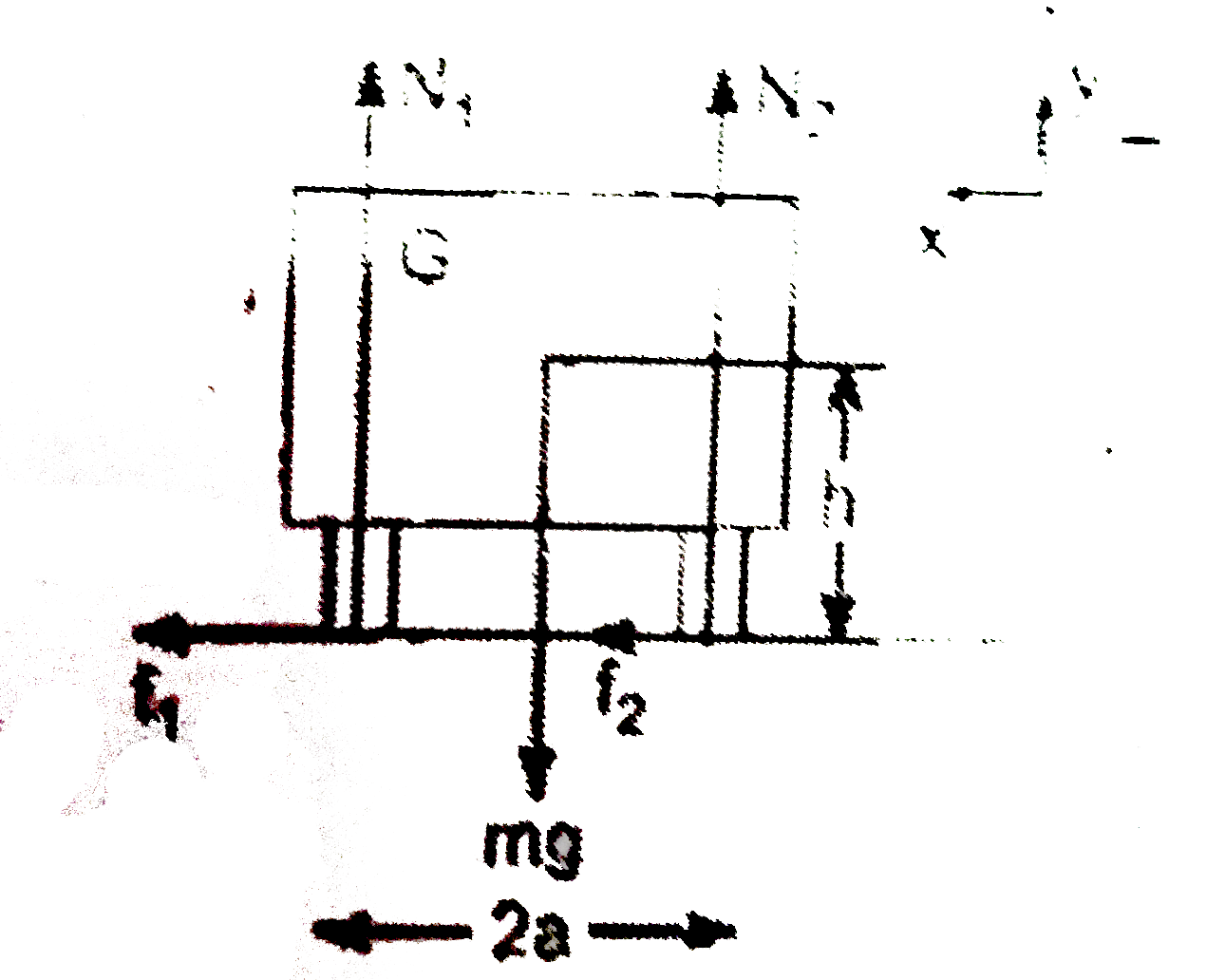
View SolutionA car of mass m is moving on a level circular track of radius R if μs represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by.
View Solution
Knowledge Check
A car of mass m is moving on a level circular track of radius R, if μs represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by.
A√μsmRgB√Rg/μsC√mRg/μsD√μsRgA car of mass m is moving on a level circular track of radius R. If μs represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by
A√μsRgB√RgμsC√mRgμsD√(μsRg)The centre of gravity of a car is at a height h and the distance between its wheel is 2a. The car moves on a level curve of radius r with speed v. Let N1andN2 be the normal reactions on the inner and outer wheels of the car. Then
AN1>N2BN2>N1CN1=N2Dthe maximum value of v to avoid overturning is √argh
For a car taking a turn on a horizontal surface, let N1 and N2 be the normal reactions of the road on the inner and outer wheels respectively
View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground h, and the separation between its inner and outer wheel, is d. The road is dry, and the car does not skid. Show that the maximum speed the car can have without overturning is given by vmax=√gRd2h. To reduce the risk of rollover, should one increase or decrease h? Should one increase or decrease the width d of the wheel base?

View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .
.
View SolutionA body of mass m is moving in a circle of radius r with a constant speed v, The force on the body is mv2r and is directed towards the centre what is the work done by the from in moving the body over half the circumference of the circle?
View Solution
