A cylinder has a surface area of 360π units square, and is 3 units tall. What is the diameter of the cylinder's circular base?
To find the diameter of the circular base of a cylinder with a given surface area and height, we can follow these steps:
Step 1: Understand the formula for the surface area of a cylinder
The surface area A of a cylinder is given by the formula:
A=2πrh+2πr2
where r is the radius of the base, h is the height, and 2πr2 accounts for the area of the two circular bases.
Step 2: Substitute the known values into the formula
Given that the surface area A=360π and the height h=3 units, we can substitute these values into the formula:
360π=2πr(3)+2πr2
Step 3: Simplify the equation
First, we can factor out 2π from the right side:
360π=2π(3r+r2)
Now, divide both sides by 2π:
180=3r+r2
Step 4: Rearrange the equation
Rearranging gives us a standard quadratic equation:
r2+3r−180=0
Step 5: Solve the quadratic equation
To solve for r, we can use the quadratic formula:
r=−b±√b2−4ac2a
Here, a=1, b=3, and c=−180:
r=−3±√32−4⋅1⋅(−180)2⋅1
r=−3±√9+7202
r=−3±√7292
r=−3±272
Calculating the two possible values for r:
1. r=242=12
2. r=−302=−15 (not valid since radius cannot be negative)
Thus, r=12.
Step 6: Calculate the diameter
The diameter d of the circular base is given by:
d=2r=2×12=24
Final Answer
The diameter of the cylinder's circular base is 24 units.
---
The surface area A of a cylinder is given by the formula:
A=2πrh+2πr2
where r is the radius of the base, h is the height, and 2πr2 accounts for the area of the two circular bases.
Given that the surface area A=360π and the height h=3 units, we can substitute these values into the formula:
360π=2πr(3)+2πr2
First, we can factor out 2π from the right side:
360π=2π(3r+r2)
Now, divide both sides by 2π:
180=3r+r2
Rearranging gives us a standard quadratic equation:
r2+3r−180=0
To solve for r, we can use the quadratic formula:
r=−b±√b2−4ac2a
Here, a=1, b=3, and c=−180:
r=−3±√32−4⋅1⋅(−180)2⋅1
r=−3±√9+7202
r=−3±√7292
r=−3±272
1. r=242=12
2. r=−302=−15 (not valid since radius cannot be negative)
The diameter d of the circular base is given by:
d=2r=2×12=24
The diameter of the cylinder's circular base is 24 units.
Similar Questions
Knowledge Check
If a right circular cone has a lateral surface area of 6π and a slant height of 6, what is the radius of the base ?
A0.50B0.75C1.00D1.25
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2. Find the volume of the cylinder (in. cm3).
View Solution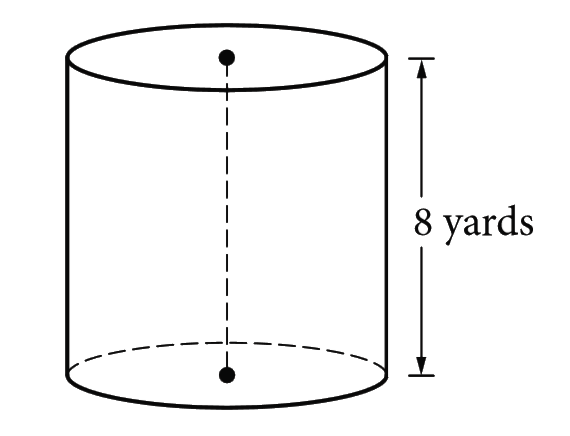
A dairy farmer uses a storage silo that is in the shape of the right circular cylinder above. If the volume of the silo is 72π cubic yards, what is the diameter–––––––––– of the base of the cylinder, in yards?
View SolutionA circular cylinder has an inextensible string wrapped around it as shown in figure. What is the linear acceleration of the cylinder when released?

View SolutionProve that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
View SolutionA given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order for the total surface area to be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π+2).
View SolutionAn oil tank has the shape of a right circular cylinder is 12 centimeters in height and has a volume of 108π cubic centimeters. What is the diameter of the base of the cylinder, in centimeters?
View SolutionThe ration between the curved surface area and the total surface area of a right circular cylinder is 1:2. Find the volume of the cylinder, if its total surface area is 616 cm2.
View Solution
