A circular hole with radius R/2 is carved from a uniform circular disk of radius R. A smaller disk with radius R/4 with the same uniform density is then put inside the hole as shown in the figure below. The center of mass of the whole system is located at a distance d from the origin. Find d. CM
Step by step video & image solution for A circular hole with radius R/2 is carved from a uniform circular disk of radius R. A smaller disk with radius R/4 with the same uniform density is then put inside the hole as shown in the figure below. The center of mass of the whole system is located at a distance d from the origin. Find d. CM by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
From a uniform circular plate of radius R, a small circular plate of radius R/4 is cut off as shown. If O is the center of the complete plate, then the x coordinate of the new center of mass of the remaining plate will be: X o Y
View SolutionA uniform disc of radius R is put over another uniform disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View Solution
Knowledge Check
- Question 1 - Select One
A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
Ar5Br4Cr2Dr3 - Question 2 - Select One
A sector cut from a uniform disk of radius 12cm and a uniform rod of the same mass bent into shape of an arc are arranged facing each other as shown in the figure. If center of mass of the combination is at the origin, what is the raius of the arc?
 A8cmB9cmC12cmD18cm
A8cmB9cmC12cmD18cm - Question 3 - Select One
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
A13B12C16D14
From a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
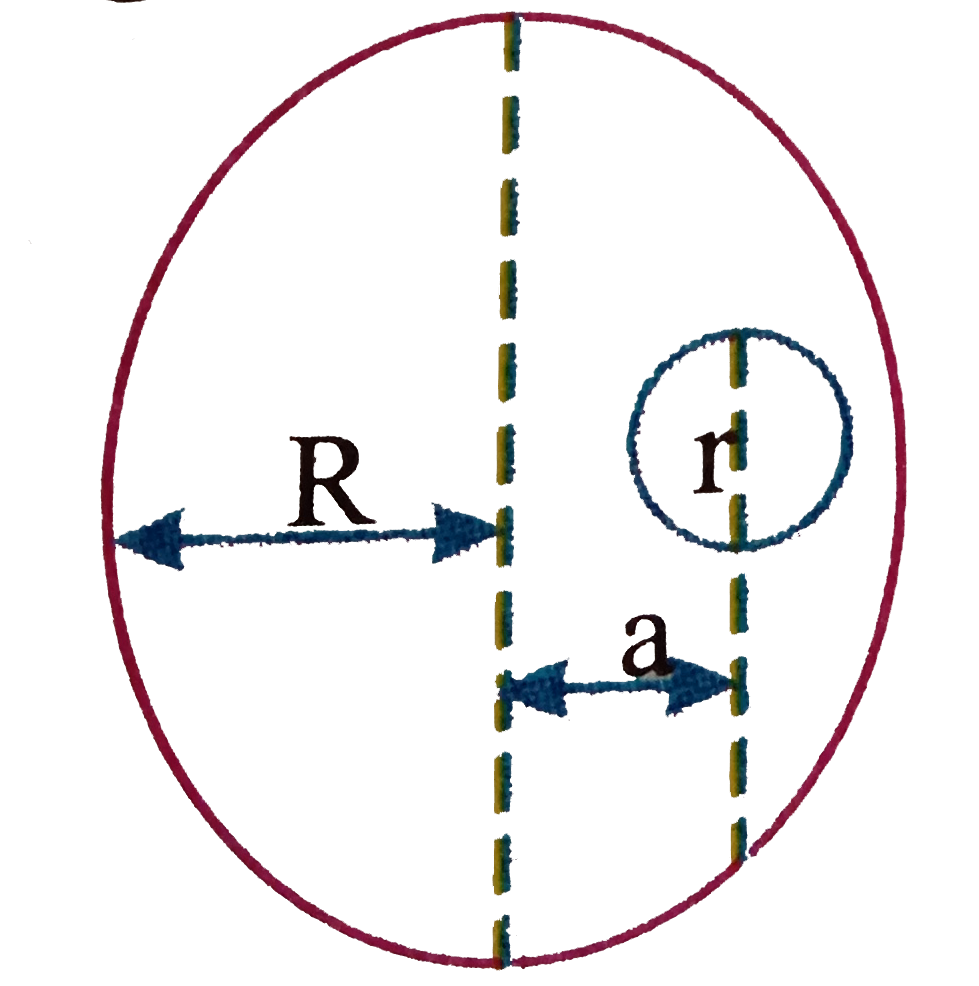 View Solution
View Solution
